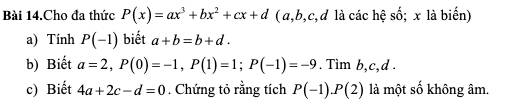Question

Answer 1

a: Sửa đề: a+c=b+d

\(P\left(-1\right)=a\cdot\left(-1\right)^3+b\cdot\left(-1\right)^2+c\cdot\left(-1\right)+d\)

=-a+b-c+d

=b+d-(a+c)

=0

b: a=2 thì \(P\left(x\right)=2x^3+bx^2+cx+d\)

P(0)=-1

=>\(2\cdot0^3+b\cdot0^2+c\cdot0+d=-1\)

=>d=-1

=>\(P\left(x\right)=2x^3+bx^2+cx-1\)

P(1)=1 và P(-1)=-9

=>\(\left\{{}\begin{matrix}2\cdot1^3+b\cdot1^2+c\cdot1-1=1\\2\cdot\left(-1\right)^3+b\cdot\left(-1\right)^2+c\cdot\left(-1\right)-1=-9\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}b+c=1+1-2=0\\b-c=-9+1+2=-6\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}b=-3\\c=3\end{matrix}\right.\)