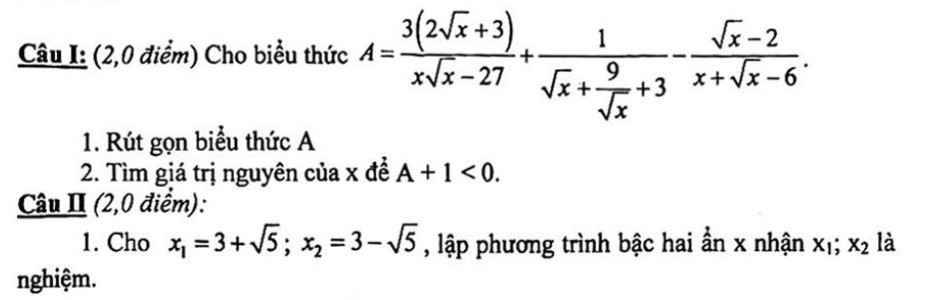Câu I:
1: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\notin\left\{9;4\right\}\end{matrix}\right.\)
\(A=\dfrac{3\left(2\sqrt{x}+3\right)}{x\sqrt{x}-27}+\dfrac{1}{\sqrt{x}+\dfrac{9}{\sqrt{x}}+3}-\dfrac{\sqrt{x}-2}{x+\sqrt{x}-6}\)
\(=\dfrac{6\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(x+3\sqrt{x}+9\right)}+1:\dfrac{x+9+3\sqrt{x}}{\sqrt{x}}-\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{6\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(x+3\sqrt{x}+9\right)}+\dfrac{\sqrt{x}}{x+3\sqrt{x}+9}-\dfrac{1}{\sqrt{x}+3}\)
\(=\dfrac{6\sqrt{x}+9+\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(x+3\sqrt{x}+9\right)}-\dfrac{1}{\sqrt{x}+3}\)
\(=\dfrac{x+3\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(x+3\sqrt{x}+9\right)}-\dfrac{1}{\sqrt{x}+3}\)
\(=\dfrac{1}{\sqrt{x}-3}-\dfrac{1}{\sqrt{x}+3}=\dfrac{\sqrt{x}+3-\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{6}{x-9}\)
2: A+1<0
=>\(\dfrac{6+x-9}{x-9}< 0\)
=>\(\dfrac{x-3}{x-9}< 0\)
=>3<x<9
mà x nguyên
nên \(x\in\left\{4;5;6;7;8\right\}\)
kết hợp ĐKXĐ, ta được: \(x\in\left\{5;6;7;8\right\}\)
1: \(x_1+x_2=3+\sqrt{5}+3-\sqrt{5}=6\)
\(x_1\cdot x_2=\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)=9-5=4\)
Phương trình bậc hai cần tìm là:
\(y^2-6y+4=0\)