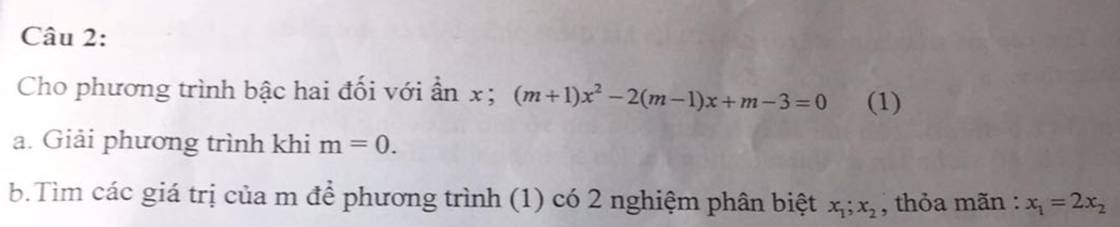\(\left(m+1\right)x^2-2\left(m-1\right)x+m-3\left(1\right)\)
a) Khi m=0 thì:
\(\left(0+1\right)x^2-2\left(0-1\right)x+0-3=0\)
\(\Leftrightarrow x^2+2x-3=0\)
\(\Delta=2^2-4\cdot1\cdot-3=16>0\)
\(x_1=\dfrac{-2+\sqrt{16}}{2}=1\)
\(x_2=\dfrac{-2-\sqrt{16}}{2}=-3\)
b) Theo vi-ét của pt (1) và đề bài đã cho ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{m+1}\\x_1x_2=\dfrac{m-3}{m+1}\\x_1=2x_2\end{matrix}\right.\)
\(\Rightarrow2x_2+x_2=\dfrac{2\left(m-1\right)}{m+1}\)
\(\Leftrightarrow3x_2=\dfrac{2\left(m-1\right)}{m+1}\)
\(\Leftrightarrow x_2=\dfrac{2\left(m-1\right)}{3\left(m+1\right)}\)
Mà: \(\Rightarrow x_1=\dfrac{m-3}{m+1}:\dfrac{2\left(m-1\right)}{3\left(m+1\right)}=\dfrac{3\left(m-3\right)}{2\left(m-1\right)}\)
\(x_1=2x_2\)
\(\Leftrightarrow\dfrac{3\left(m-3\right)}{2\left(m-1\right)}=2\cdot\dfrac{2\left(m-1\right)}{3\left(m+1\right)}\)
\(\Leftrightarrow8\left(m-1\right)^2=9\left(m+1\right)\left(m-3\right)\)
\(\Leftrightarrow8\left(m^2-2m+1\right)=9\left(m^2-2m-3\right)\)
\(\Leftrightarrow8m^2-16m+8=9m^2-18m-27\)
\(\Leftrightarrow m^2-2m-35=0\)
\(\Delta=\left(-2\right)^2-4\cdot1\cdot-35=144>0\)
\(m_1=\dfrac{2+\sqrt{144}}{2}=7\)
\(m_2=\dfrac{2-\sqrt{144}}{2}=-5\)
Vậy: ...