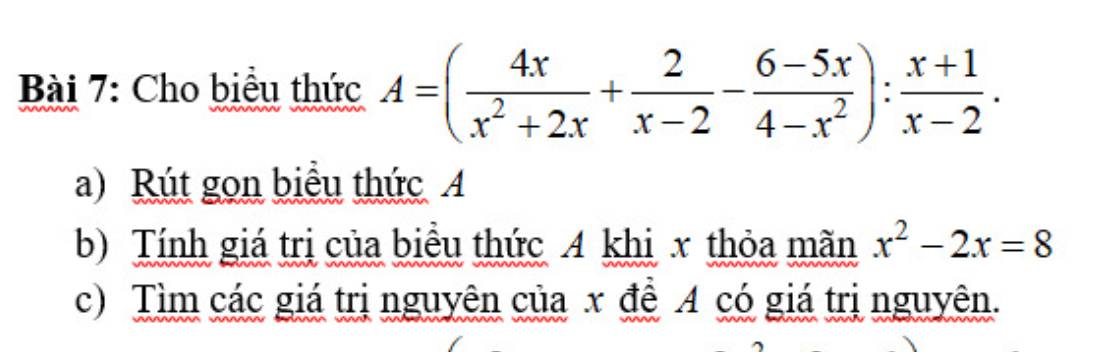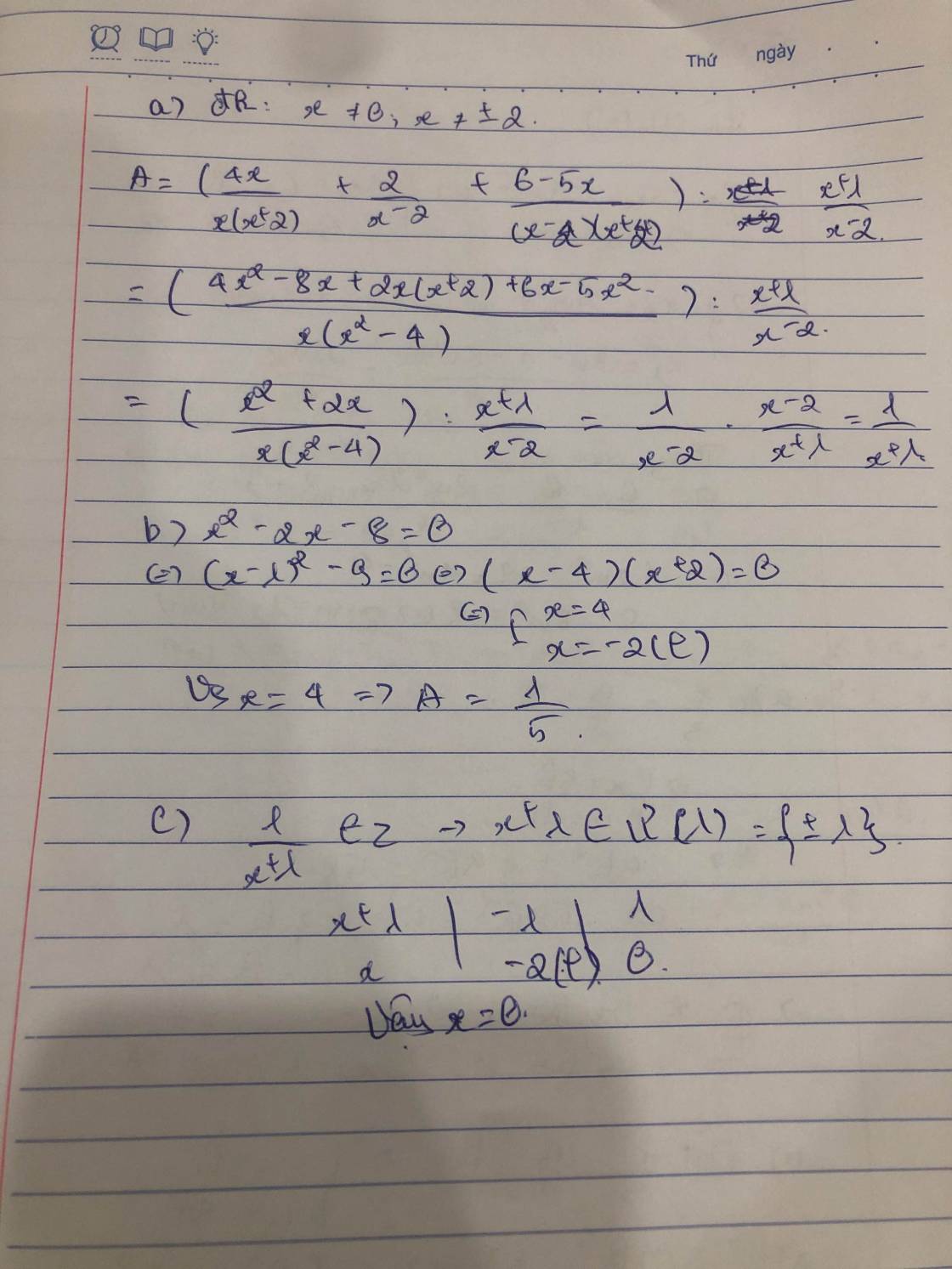Lời giải:
a. ĐKXĐ: $x\neq -1; x\neq \pm 2$
\(A=\left[\frac{4x}{x(x+2)}+\frac{2}{x-2}+\frac{6-5x}{(x-2)(x+2)}\right].\frac{x-2}{x+1}\\ =\left[\frac{4}{x+2}+\frac{2}{x-2}+\frac{6-5x}{(x-2)(x+2)}\right].\frac{x-2}{x+1}\\ =\frac{4(x-2)+2(x+2)+(6-5x)}{(x-2)(x+2)}.\frac{x-2}{x+1}\\ =\frac{x+2}{(x-2)(x+2)}.\frac{x-2}{x+1}=\frac{1}{x+1}\)
b.
$x^2-2x=8$
$\Leftrightarrow x^2-2x-8=0$
$\Leftrightarrow (x+2)(x-4)=0$
$\Leftrightarrow x=-2$ hoặc $x=4$. Do $x\neq -2$ nên $x=4$
Khi đó: $A=\frac{1}{x+1}=\frac{1}{4+1}=\frac{1}{5}$
c.
Với $x$ nguyên, để $A=\frac{1}{x+1}$ nguyên thì $1\vdots x+1$
$\Rightarrow x+1\in \left\{\pm 1\right\}$
$\Rightarrow x\in \left\{0; -2\right\}$
Do $x\neq -2$ nên $x=0$