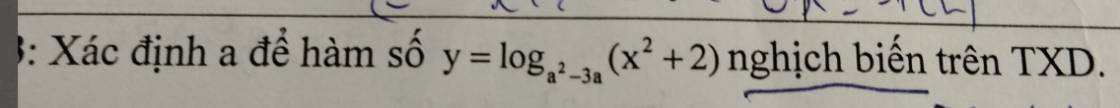ĐKXĐ: \(\left\{{}\begin{matrix}0< a^2-3a\\a^2-3a\ne1\\x^2+2>0\left(luônđúng\right)\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a\left(a-3\right)>0\\a^2-3a-1< >0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}a>3\\a< 0\end{matrix}\right.\\a\notin\left\{\dfrac{3+\sqrt{13}}{2};\dfrac{3-\sqrt{13}}{2}\right\}\end{matrix}\right.\)
Để hàm số \(y=log_{a^2-3a}\left(x^2+2\right)\) nghịch biến trên TXĐ thì \(0< a^2-3a< 1\)
=>\(\left\{{}\begin{matrix}a^2-3a>0\\a^2-3a-1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}a>3\\a< 0\end{matrix}\right.\\\dfrac{3-\sqrt{13}}{2}< a< \dfrac{3+\sqrt{13}}{2}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\dfrac{3-\sqrt{13}}{2}< a< 0\\3< a< \dfrac{3+\sqrt{13}}{2}\end{matrix}\right.\)