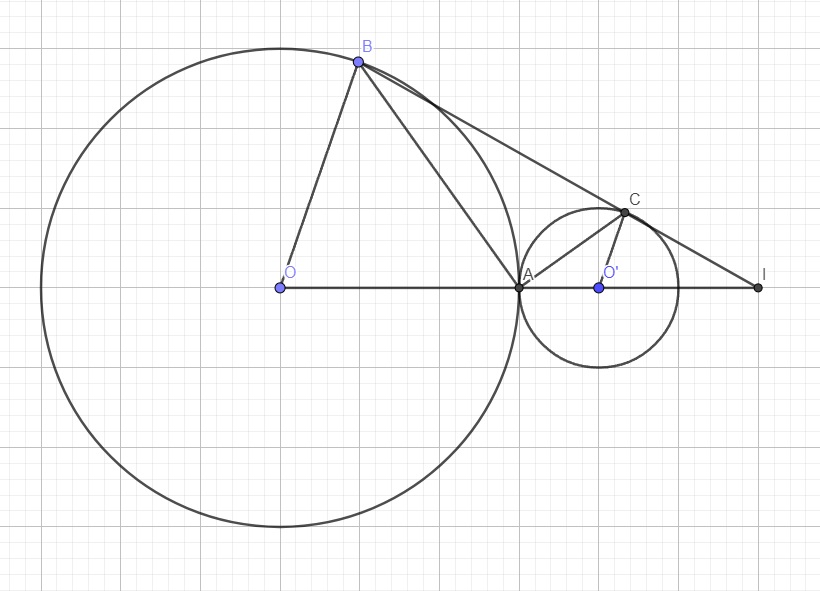
a.
Do \(OB||O'C\Rightarrow\widehat{BOA}+\widehat{CO'A}=180^0\) (hai góc trong cùng phía)
Mà \(\left\{{}\begin{matrix}OA=OB=3\\O'A=OC'=1\end{matrix}\right.\) \(\Rightarrow\) các tam giác OAB và O'AC lần lượt cân tại O và O'
\(\Rightarrow\left\{{}\begin{matrix}\widehat{OBA}=\widehat{OAB}\\\widehat{O'CA}=\widehat{O'AC}\end{matrix}\right.\)
\(\Rightarrow\widehat{BAC}=180^0-\left(\widehat{OAB}+\widehat{O'CA}\right)=180^0-\left(\dfrac{180^0-\widehat{BOA}}{2}+\dfrac{180^0-\widehat{CO'A}}{2}\right)\)
\(=180^0-\left(180^0-\dfrac{\widehat{BOA}+\widehat{CO'A}}{2}\right)=90^0\)
b.
Do \(O'C||OB\), áp dụng định lý Thales:
\(\dfrac{O'C}{OB}=\dfrac{IO'}{OI}=\dfrac{OI-OO'}{OI}=\dfrac{OI-\left(OA+OA'\right)}{OI}\)
\(\Rightarrow\dfrac{1}{3}=1-\dfrac{4}{OI}\Rightarrow\dfrac{4}{OI}=\dfrac{2}{3}\)
\(\Rightarrow OI=6\) (cm)