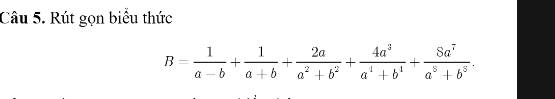\(B=\dfrac{1}{a-b}+\dfrac{1}{a+b}+\dfrac{2a}{a^2+b^2}+\dfrac{4a^3}{a^4+b^4}+\dfrac{8a^7}{a^8+b^8}\)
\(=\dfrac{a+b+a-b}{\left(a-b\right)\left(a+b\right)}+\dfrac{2a}{a^2+b^2}+\dfrac{4a^3}{a^4+b^4}+\dfrac{8a^7}{a^8+b^8}\)
\(=\dfrac{2a}{a^2-b^2}+\dfrac{2a}{a^2+b^2}+\dfrac{4a^3}{a^4+b^4}+\dfrac{8a^7}{a^8+b^8}\)
\(=\dfrac{2a\left(a^2+b^2\right)+2a\left(a^2-b^2\right)}{\left(a^2-b^2\right)\left(a^2+b^2\right)}+\dfrac{4a^3}{a^4+b^4}+\dfrac{8a^7}{a^8+b^8}\)
\(=\dfrac{4a^3}{a^4-b^4}+\dfrac{4a^3}{a^4+b^4}+\dfrac{8a^7}{a^8+b^8}\)
\(=\dfrac{4a^3\left(a^4+b^4\right)+4a^3\left(a^4-b^4\right)}{a^8-b^8}+\dfrac{8a^7}{a^8+b^8}\)
\(=\dfrac{8a^7}{a^8-b^8}+\dfrac{8a^7}{a^8+b^8}\)
\(=\dfrac{8a^7\left(a^8+b^8\right)+8a^7\left(a^8-b^8\right)}{a^{16}-b^{16}}\)
\(=\dfrac{16a^{15}}{a^{16}-b^{16}}\)