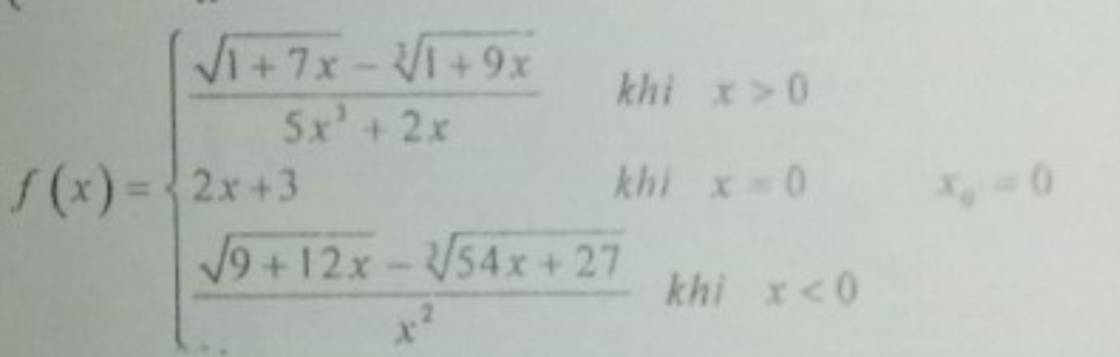\(\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{1+7x}-\sqrt[3]{1+9x}}{5x^3+2x}=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{1+7x}-1+1-\sqrt[3]{1+9x}}{x\left(5x^2+2\right)}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{7x}{\sqrt[]{1+7x}+1}+\dfrac{9x}{1+\sqrt[3]{9x+1}+\sqrt[3]{\left(9x+1\right)^2}}}{x\left(5x^2+2\right)}=\dfrac{\dfrac{7}{2}+\dfrac{9}{3}}{2}=\dfrac{13}{4}\)
\(\lim\limits_{x\rightarrow0^-}\dfrac{\sqrt[]{9+12x}-\sqrt[3]{54x+27}}{x^2}=\lim\limits_{x\rightarrow0^-}\dfrac{\sqrt[]{9+12x}-\left(2x+3\right)+\left(2x+3-\sqrt[3]{54x+27}\right)}{x^2}\)
\(=\lim\limits_{x\rightarrow0^-}\dfrac{\dfrac{-4x^2}{\sqrt[]{9+12x}+2x+3}+\dfrac{4x^2\left(2x+9\right)}{\left(2x+3\right)^2+\left(2x+3\right)\sqrt[3]{54x+27}+\sqrt[3]{\left(54x+27\right)^2}}}{x^2}\)
\(=\dfrac{-4}{3+3}+\dfrac{9}{9+9+9}=-\dfrac{1}{3}\)
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)\ne\lim\limits_{x\rightarrow0^-}f\left(x\right)\) nên ko tồn tại \(\lim\limits_{x\rightarrow0}f\left(x\right)\)