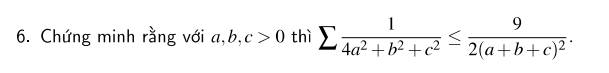\(a,b,c>0\)
\(\sum\dfrac{1}{4a^2+b^2+c^2}\le\dfrac{9}{2\left(a+b+c\right)^2}\Leftrightarrow\sum\dfrac{\left(a+b+c\right)^2}{4a^2+b^2+c^2}\le\dfrac{9}{2}\)
Áp dụng bất đẳng thức CBS, ta có:
\(\sum\dfrac{\left(a+b+c\right)^2}{4a^2+b^2+c^2}\le\sum\left(\dfrac{a^2}{2a^2}+\dfrac{b^2}{a^2+b^2}+\dfrac{c^2}{a^2+c^2}\right)=\dfrac{1}{2}\sum\dfrac{a^2}{a^2}+\sum\dfrac{a^2+b^2}{a^2+b^2}=3+\dfrac{3}{2}=\dfrac{9}{2}\left(đpcm\right)\)
Đẳng thức xảy ra khi \(a=b=c\)
Đúng 0
Bình luận (0)
