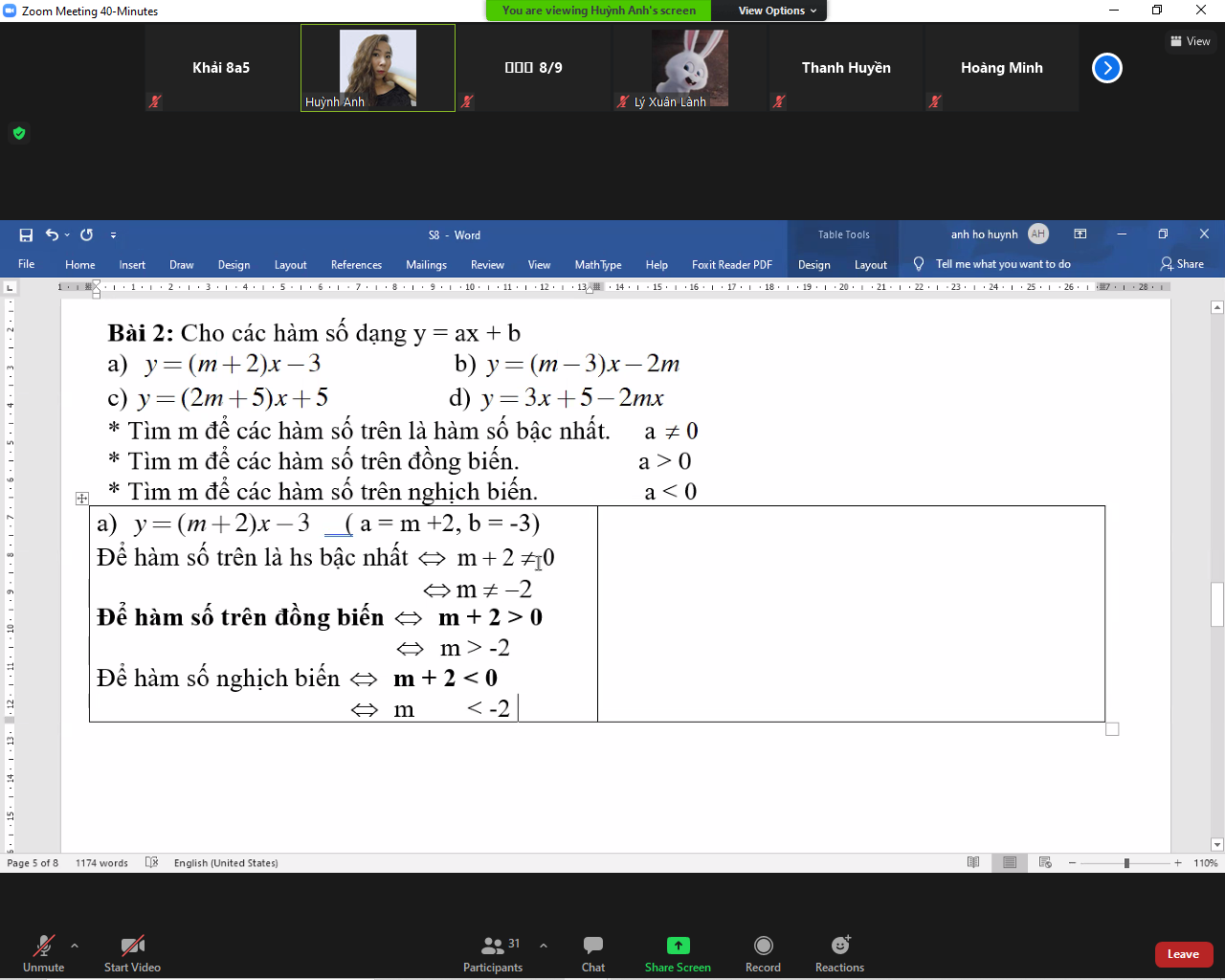
a: Thay x=1 và y=2 vào (d), ta được:
\(1\left(3m-2\right)+m-2=2\)
=>4m-4=2
=>4m=4+2=6
=>\(m=\dfrac{6}{4}=\dfrac{3}{2}\)
Khi m=3/2 thì \(y=\left(3\cdot\dfrac{3}{2}-2\right)x+\dfrac{3}{2}-2=\dfrac{5}{2}x-\dfrac{1}{2}\)
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\left(3m-2\right)x+m-2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\x\left(3m-2\right)=-m+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=\dfrac{-m+2}{3m-2}\end{matrix}\right.\)
=>\(A\left(\dfrac{-m+2}{3m-2};0\right)\)
\(OA=\sqrt{\left(\dfrac{-m+2}{3m-2}-0\right)^2+\left(0-0\right)^2}=\sqrt{\left(\dfrac{-m+2}{3m-2}\right)^2}=\dfrac{\left|m-2\right|}{\left|3m-2\right|}\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=\left(3m-2\right)\cdot x+m-2=0\left(3m-2\right)+m-2=m-2\end{matrix}\right.\)
=>\(B\left(0;m-2\right)\)
\(OB=\sqrt{\left(0-0\right)^2+\left(m-2-0\right)^2}=\sqrt{0^2+\left(m-2\right)^2}=\left|m-2\right|\)
Ox\(\perp\)Oy
=>OA\(\perp\)OB
=>ΔOAB vuông tại O
=>\(S_{AOB}=\dfrac{1}{2}\cdot OA\cdot OB\)
=>\(S_{OAB}=\dfrac{1}{2}\cdot\dfrac{\left|m-2\right|}{\left|3m-2\right|}\cdot\left|m-2\right|\)
=>\(S_{AOB}=\dfrac{\dfrac{1}{2}\left(m-2\right)^2}{\left|3m-2\right|}\)
Để \(S_{AOB}=\dfrac{1}{2}\) thì \(\dfrac{1}{2}\cdot\dfrac{\left(m-2\right)^2}{\left|3m-2\right|}=\dfrac{1}{2}\)
=>\(\left(m-2\right)^2=\left|3m-2\right|\)
=>\(\left\{{}\begin{matrix}3m-2>0\\\left(m-2\right)^2=3m-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m^2-4m+4-3m+2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m^2-7m+6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\\left(m-1\right)\left(m-6\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>\dfrac{2}{3}\\\left[{}\begin{matrix}m-1=0\\m-6=0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\\left[{}\begin{matrix}m=1\left(nhận\right)\\m=6\left(nhận\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy: \(m\in\left\{1;6\right\}\)
c: (d): \(y=\left(3m-2\right)x+m-2\)
\(=3mx-2x+m-2\)
\(=m\left(3x+1\right)-2x-2\)
Tọa độ điểm cố định mà (d) luôn đi qua là:
\(\left\{{}\begin{matrix}3x+1=0\\y=-2x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{3}\\y=-2\cdot\dfrac{-1}{3}-2=\dfrac{2}{3}-2=-\dfrac{4}{3}\end{matrix}\right.\)