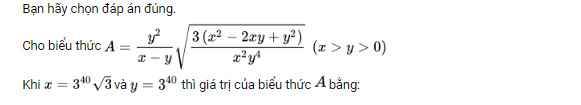Question

Answer 1

x>y>0

=>x-y>0

\(A=\dfrac{y^2}{x-y}\cdot\sqrt{\dfrac{3\left(x^2-2xy+y^2\right)}{x^2y^4}}\)

\(=\dfrac{y^2}{x-y}\cdot\sqrt{\dfrac{3\left(x-y\right)^2}{\left(xy^2\right)^2}}\)

=>\(A=\dfrac{y^2}{x-y}\cdot\sqrt{3}\cdot\dfrac{\left|x-y\right|}{\left|xy^2\right|}\)

\(=\sqrt{3}\cdot\dfrac{y^2}{x-y}\cdot\dfrac{x-y}{xy^2}=\dfrac{\sqrt{3}}{x}=\dfrac{\sqrt{3}}{\sqrt{3}\cdot3^{40}}=\dfrac{1}{3^{40}}\)