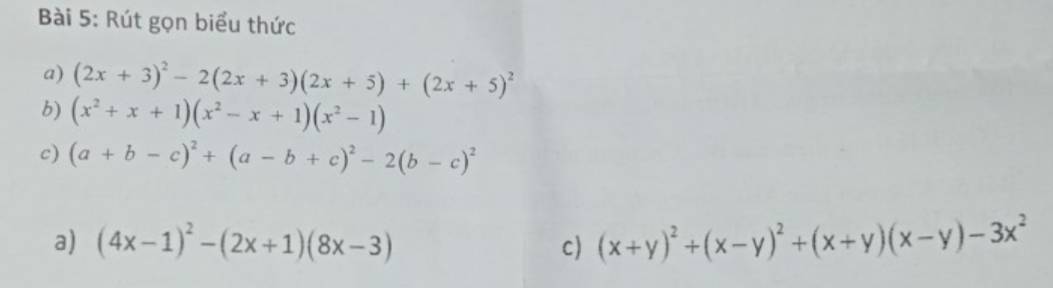\(a,(2x+3)^2-2(2x+3)(2x+5)+(2x+5)^2\\=[(2x+3)-(2x+5)]^2\\=(2x+3-2x-5)^2\\=(-2)^2=4\\---\\b,(x^2+x+1)(x^2-x+1)(x^2-1)\\=(x^2+x+1)(x^2-x+1)(x-1)(x+1)\\=[(x-1)(x^2+x+1)][(x+1)(x^2-x+1)]\\=(x^3-1)(x^3+1)\\=x^6-1\\---\)
\(c,(a+b-c)^2+(a-b+c)^2-2(b-c)^2\\=[a+(b-c)]^2+[a-(b-c)]^2-2(b-c)^2\)
Đặt \(b-c=y\), khi đó ta được:
\((a+y)^2+(a-y)^2-2y^2\\=a^2+2ay+y^2+a^2-2ay+y^2-2y^2\\=2a^2\)
\(\text{#}Toru\)
\(a,(4x-1)^2-(2x+1)(8x-3)\\=(4x)^2-2\cdot4x\cdot1+1^2-(16x^2-6x+8x-3)\\=16x^2-8x+1-(16x^2+2x-3)\\=16x^2-8x+1-16x^2-2x+3\\=-10x+4\\---\\c,(x+y)^2+(x-y)^2+(x+y)(x-y)-3x^2\\=x^2+2xy+y^2+x^2-2xy+y^2+x^2-y^2-3x^2\\=y^2\)