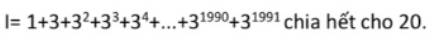Question

Answer 1

\(I=1+3+3^2+3^3+3^4+...+3^{1990}+3^{1991}\\=(1+3+3^2+3^3)+(3^4+3^5+3^6+3^7)+...+(3^{1988}+3^{1989}+3^{1990}+3^{1991})\\=40+3^4\cdot(1+3+3^2+3^3)+...+3^{1989}\cdot(1+3+3^2+3^3)\\=40+3^4\cdot40+...+3^{1989}\cdot40\\=40\cdot(1+3^4+...+3^{1989})\)

Vì \(40\vdots20\) nên \(40\cdot(1+3^4+...+3^{1989}\vdots20\)

hay \(I\vdots20\).