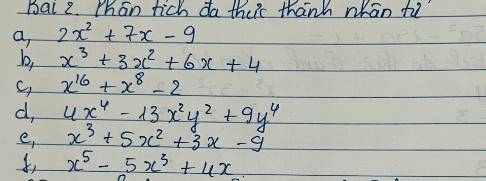a) 2x² + 7x - 9
= 2x² - 2x + 9x - 9
= (2x² - 2x) + (9x - 9)
= 2x(x - 1) + 9(x - 1)
= (x - 1)(2x + 9)
b) x³ + 3x² + 6x + 4
= x³ + 3x² + 3x + 1 + 3x + 3
= (x³ + 3x² + 3x + 1) + (3x + 3)
= (x + 1)³ + 3(x + 1)
= (x + 1)[(x + 1)² + 3]
= (x + 1)(x² + 2x + 1 + 3)
= (x + 1)(x² + 2x + 4)
c) x¹⁶ + x⁸ - 2
= x¹⁶ - x⁸ + 2x⁸ - 2
= (x¹⁶ - x⁸) + (2x⁸ - 2)
= x⁸(x⁸ - 1) + 2(x⁸ - 1)
= (x⁸ - 1)(x⁸ + 2)
= (x⁴ - 1)(x⁴ + 1)(x⁸ + 2)
= (x² - 1)(x² + 1)(x⁴ + 1)(x⁸ + 2)
= (x - 1)(x + 1)(x² + 1)(x⁴ + 1)(x⁸ + 2)
d) 4x⁴ - 13x²y² + 9y⁴
= 4x⁴ - 4x²y² - 9x²y² + 9y⁴
= (4x⁴ - 4x²y²) - (9x²y² - 9y⁴)
= 4x²(x² - y²) - 9y²(x² - y²)
= (x² - y²)(4x² - 9y²)
= (x - 1)(x + 1)(2x - 3y)(2x + 3y)
e) x³ + 5x² + 3x - 9
= x³ - x² + 6x² - 6x + 9x - 9
= (x³ - x²) + (6x² - 6x) + (9x - 9)
= x²(x - 1) + 6x(x - 1) + 9(x - 1)
= (x - 1)(x² + 6x + 9)
= (x - 1)(x + 3)²
f) x⁵ - 5x³ + 4x
= x(x⁴ - 5x² + 4)
= x(x⁴ - x² - 4x² + 4)
= x[(x⁴ - x²) - (4x² - 4)]
= x[x²(x² - 1) - 4(x² - 1)]
= x(x² - 1)(x² - 4)
= x(x - 1)(x + 1)(x - 2)(x + 2)