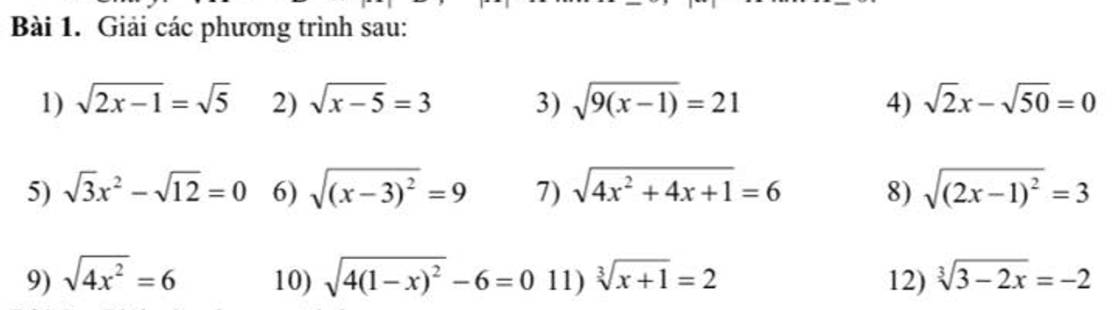1: ĐKXĐ: 2x-1>=0
=>x>=1/2
\(\sqrt{2x-1}=\sqrt{5}\)
=>2x-1=5
=>2x=6
=>x=3
2: ĐKXĐ: x>=5
\(\sqrt{x-5}=3\)
=>x-5=9
=>x=14
3: ĐKXĐ: x>=1
\(\sqrt{9\left(x-1\right)}=21\)
=>\(3\sqrt{x-1}=21\)
=>\(\sqrt{x-1}=7\)
=>x-1=49
=>x=50
4: ĐKXĐ: \(x\in R\)
\(x\sqrt{2}-\sqrt{50}=0\)
=>\(x\sqrt{2}-5\sqrt{2}=0\)
=>x-5=0
=>x=5
5: ĐKXĐ: \(x\in R\)
\(x^2\sqrt{3}-\sqrt{12}=0\)
=>\(x^2\cdot\sqrt{3}=2\sqrt{3}\)
=>x^2=2
=>\(x=\pm\sqrt{2}\)
6: ĐKXĐ: \(x\in R\)
\(\sqrt{\left(x-3\right)^2}=9\)
=>|x-3|=9
=>\(\left[{}\begin{matrix}x-3=9\\x-3=-9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=12\\x=-6\end{matrix}\right.\)
7: ĐKXĐ: \(x\in R\)
\(\sqrt{4x^2+4x+1}=6\)
=>\(\sqrt{\left(2x+1\right)^2}=6\)
=>|2x+1|=6
=>\(\left[{}\begin{matrix}2x+1=6\\2x+1=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{7}{2}\end{matrix}\right.\)
8: ĐKXĐ: \(x\in R\)
\(\sqrt{\left(2x-1\right)^2}=3\)
=>\(\left|2x-1\right|=3\)
=>\(\left[{}\begin{matrix}2x-1=3\\2x-1=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=4\\2x=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
9: ĐKXĐ: \(x\in R\)
\(\sqrt{4x^2}=6\)
=>\(2\sqrt{x^2}=6\)
=>\(2\left|x\right|=6\)
=>\(\left|x\right|=3\)
=>x=3 hoặc x=-3
10: ĐKXĐ: \(x\in R\)
\(\sqrt{4\left(1-x\right)^2}-6=0\)
=>\(\sqrt{\left[2\left(x-1\right)\right]^2}-6=0\)
=>\(\left|2\cdot\left(x-1\right)\right|-6=0\)
=>\(\left|x-1\right|=3\)
=>x-1=3 hoặc x-1=-3
=>x=4 hoặc x=-2
11: ĐKXĐ: \(x\in R\)
\(\sqrt[3]{x+1}=2\)
=>x+1=8
=>x=7
12: ĐKXĐ: \(x\in R\)
\(\sqrt[3]{3-2x}=-2\)
=>3-2x=-8
=>2x=11
=>x=11/2