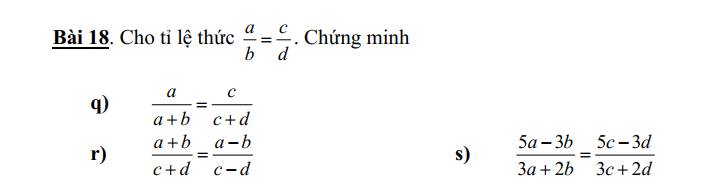\(q,\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow ad=bc\)
\(\Leftrightarrow ac+ad=ac+bc\)
\(\Leftrightarrow a\left(c+d\right)=c\left(a+b\right)\)
\(\Leftrightarrow\dfrac{a}{a+b}=\dfrac{c}{c+d}\)
\(---\)
\(r,\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\)
\(---\)
\(s,\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{5a}{5c}=\dfrac{3b}{3d}=\dfrac{5a-3b}{5c-3d}\)
\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{3a}{3c}=\dfrac{2b}{2d}=\dfrac{3a+2b}{3c+2d}\)
\(\Leftrightarrow\dfrac{5a-3b}{5c-3d}=\dfrac{3a+2b}{3c+2d}\)
\(\Leftrightarrow\dfrac{5a-3b}{3a+2b}=\dfrac{5c-3d}{3c+2d}\)
#\(Toru\)