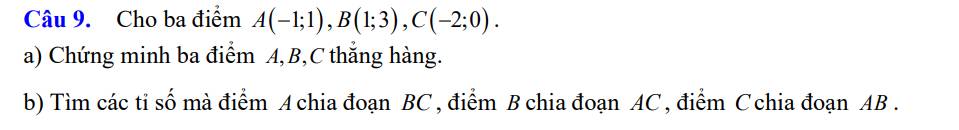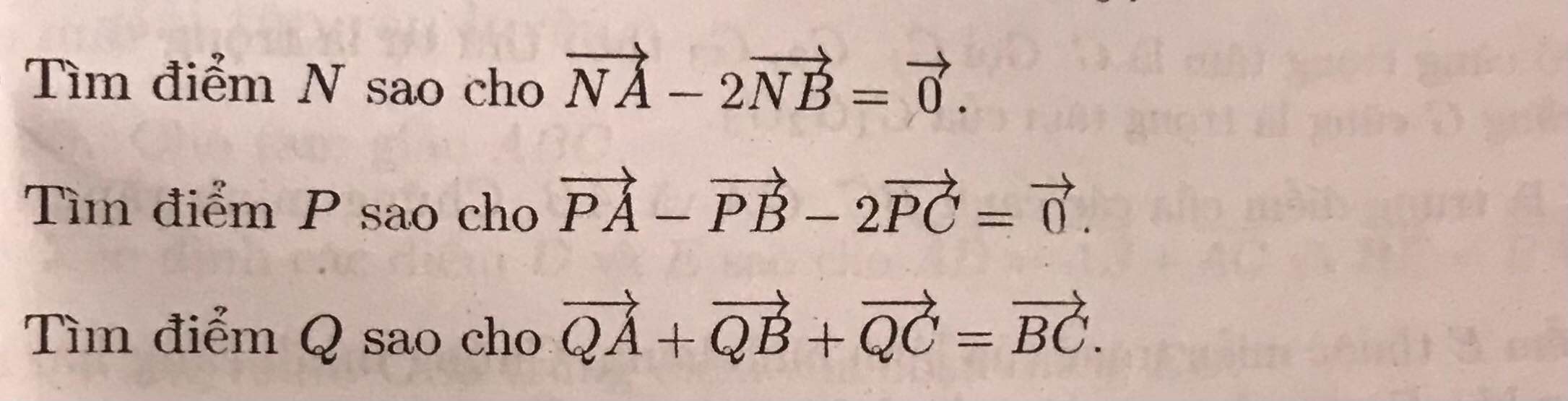Question

Answer 1

a: \(\overrightarrow{AB}=\left(2;2\right);\overrightarrow{AC}=\left(-1;-1\right)\)

Vì 2/-1=2/-1

nên A,B,C thẳng hàng

b: \(AB=\sqrt{\left(1+1\right)^2+\left(3-1\right)^2}=2\sqrt{2}\)

\(AC=\sqrt{\left(-2+1\right)^2+1^2}=\sqrt{2}\)

\(BC=\sqrt{\left(-2-1\right)^2+3^2}=3\sqrt{2}\)

\(\dfrac{AB}{AC}=\dfrac{2\sqrt{2}}{\sqrt{2}}=2\)

\(\dfrac{BA}{BC}=\dfrac{2\sqrt{2}}{3\sqrt{2}}=\dfrac{2}{3}\)

\(\dfrac{CA}{CB}=\dfrac{\sqrt{2}}{3\sqrt{2}}=\dfrac{1}{3}\)