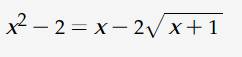\(\Leftrightarrow x^2-1=x+1-2\sqrt{x+1}\)
=>\(\left(x-1\right)\left(x+1\right)=\sqrt{x+1}\left(\sqrt{x+1}-2\right)\)
=>\(\left(\sqrt{x+1}\right)\left(\sqrt{x+1}-2\right)-\left(\sqrt{x+1}\right)\left(\sqrt{x+1}\left(x-1\right)\right)=0\)
=>\(\sqrt{x+1}\left(\sqrt{x+1}-2-\left(x-1\right)\sqrt{x+1}\right)=0\)
=>\(\sqrt{x+1}=0\)
=>x+1=0
=>x=-1
\(x^2-2=x-2\sqrt{x+1}\) (ĐK: \(x\ge-1\))
\(\Leftrightarrow x^2-1-1=x-2\sqrt{x+1}\)
\(\Leftrightarrow x^2-1=x+1-2\sqrt{x+1}\)
\(\Leftrightarrow\left(x+1\right)\left(x-1\right)=\left(x+1\right)-2\sqrt{x+1}\)
\(\Leftrightarrow\left(\sqrt{x-1}\right)^2\left(\sqrt{x+1}\right)^2=\left(\sqrt{x+1}\right)^2-2\sqrt{x+1}\)
\(\Leftrightarrow\left(\sqrt{x-1}\right)^2\left(\sqrt{x+1}\right)^2=\sqrt{x+1}\left(\sqrt{x+1}-2\right)\)
\(\Leftrightarrow\left(\sqrt{x-1}\right)^2\left(\sqrt{x+1}\right)^2-\sqrt{x+1}\left(\sqrt{x+1}-2\right)=0\)
\(\Leftrightarrow\sqrt{x+1}\left[\left(x-1\right)\left(\sqrt{x+1}\right)-\sqrt{x+1}-2\right]=0\)
Mà: \(\left(x-1\right)\left(\sqrt{x+1}\right)-\sqrt{x+1}-2\ne0\)
\(\Leftrightarrow\sqrt{x+1}=0\)
\(\Leftrightarrow x+1=0\)
\(\Leftrightarrow x=-1\left(tm\right)\)
Vậy: x=-1