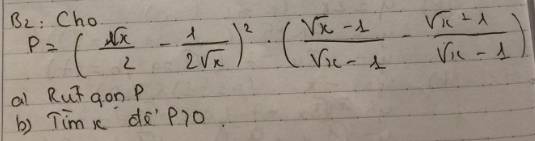a: \(P=\left(\dfrac{x-1}{2\sqrt{x}}\right)^2\cdot\dfrac{\sqrt{x}-1-\sqrt{x}-1}{\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\left(x-1\right)^2}{4x}\cdot\dfrac{-2}{\sqrt{x}-1}=\dfrac{-1}{2x}\cdot\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2\)
b: P>0
=>\(-\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}{2x}>0\)
=>\(-\left(\sqrt{x}-1\right)>0\)
=>căn x<1
=>0<x<1
a) \(P=\left(\dfrac{\sqrt{x}}{2}-\dfrac{1}{2\sqrt{x}}\right)^2\cdot\left(\dfrac{\sqrt{x}-1}{\sqrt{x}-1}+\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\right)\) (ĐK: \(x>0;x\ne1\))
\(P=\left[\dfrac{\sqrt{x}\cdot\sqrt{x}}{2\sqrt{x}}-\dfrac{1}{2\sqrt{x}}\right]^2\cdot\dfrac{\sqrt{x}-1-\sqrt{x}-1}{\sqrt{x}-1}\)
\(P=\left(\dfrac{x-1}{2\sqrt{x}}\right)^2\cdot\dfrac{-2}{\sqrt{x}-1}\)
\(P=\dfrac{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)^2}{4x}\cdot\dfrac{-2}{\sqrt{x}-1}\)
\(P=\dfrac{\left(\sqrt{x}+1\right)^2\left(x-1\right)}{-2x}\)
b) P > 0 khi:
\(\dfrac{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}{-\sqrt{x}}>0\)
Mà \(-2x\le0\) và \(\left(\sqrt{x}+1\right)^2>0\) nên:
\(\sqrt{x}-1< 0\)
\(\Leftrightarrow\sqrt{x}< 1\)
\(\Leftrightarrow x< 1\)
Kết hợp với đk:
Vậy: P > 0 khi:
\(0< x< 1\)