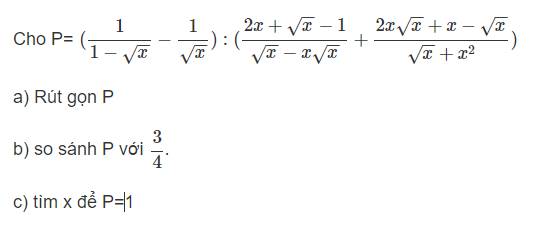a: ĐKXĐ: x>0; ,x<>1
\(P=\left(\dfrac{-1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}}\right):\left(\dfrac{\left(\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}{\sqrt{x}\left(1-x\right)}+\dfrac{2x+\sqrt{x}-1}{x\sqrt{x}+1}\right)\)
\(=\dfrac{-\sqrt{x}-\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\left[\left(\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)\left(\dfrac{1}{\sqrt{x}\left(1-x\right)}+\dfrac{1}{x\sqrt{x}+1}\right)\right]\)
\(=\dfrac{-2\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\left[\left(\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)\left(\dfrac{-x+\sqrt{x}-1+x-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\right)\right]\)
\(=\dfrac{-2\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{-\left(\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{2\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(x-\sqrt{x}+1\right)}{2\sqrt{x}-1}\)
\(=x-\sqrt{x}+1\)
b: \(P-\dfrac{3}{4}=x-\sqrt{x}+\dfrac{1}{4}=\left(\sqrt{x}-\dfrac{1}{2}\right)^2>=0\)
=>P>=3/4
c: P=1
=>\(x-\sqrt{x}=0\)
=>x=0(loại) hoặc x=1(loại)