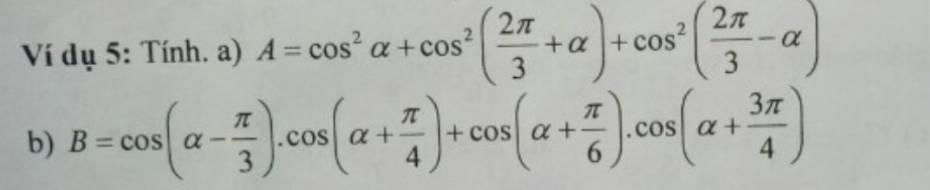b: \(B=\dfrac{1}{2}\left[cos\left(a-\dfrac{pi}{3}+a+\dfrac{pi}{4}\right)+cos\left(a-\dfrac{pi}{3}-a-\dfrac{pi}{4}\right)\right]+\dfrac{1}{2}\left[cos\left(a+\dfrac{pi}{6}+a+\dfrac{3}{4}pi\right)+cos\left(a+\dfrac{pi}{6}-a-\dfrac{3}{4}pi\right)\right]\)
\(=\dfrac{1}{2}\left(cos\left(2a-\dfrac{1}{12}pi\right)+\dfrac{-\sqrt{6}+\sqrt{2}}{4}+cos\left(2a+\dfrac{11}{12}pi\right)+\dfrac{-\sqrt{6}+\sqrt{2}}{4}\right)\)
\(=\dfrac{1}{2}\cdot\left(\dfrac{-\sqrt{6}+\sqrt{2}}{2}+2\cdot cos\left(2a-\dfrac{1}{12}pi\right)\right)\)
\(=\dfrac{-\sqrt{6}+\sqrt{2}}{4}+cos\left(2a-\dfrac{pi}{12}\right)\)
a: \(=cos^2a+\left[cos\left(\dfrac{2}{3}pi+a\right)\right]^2+\left[cos\left(\dfrac{2}{3}pi-a\right)\right]^2\)
\(=cos^2a+\left[cos\left(\dfrac{2}{3}pi\right)\cdot cosa-sin\left(\dfrac{2}{3}pi\right)\cdot sina\right]^2+\left[cos\left(\dfrac{2}{3}pi\right)\cdot cosa+sin\left(\dfrac{2}{3}pi\right)\cdot sina\right]^2\)
\(=cos^2a+\left(-\dfrac{1}{2}cosa-\dfrac{\sqrt{3}}{2}sina\right)^2+\left(-\dfrac{1}{2}cosa+\dfrac{\sqrt{3}}{2}sina\right)^2\)
\(=cos^2a+\left(\dfrac{\sqrt{3}}{2}sina+\dfrac{1}{2}cosa\right)^2+\left(\dfrac{\sqrt{3}}{2}sina-\dfrac{1}{2}cosa\right)^2\)
\(=cos^2a+2\cdot\left(\dfrac{\sqrt{3}}{2}sina\right)^2+2\left(\dfrac{1}{2}cosa\right)^2\)
\(=cos^2a+\dfrac{3}{2}\cdot sin^2a+\dfrac{1}{2}\cdot cos^2a=\dfrac{3}{2}\)