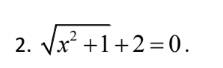\(\sqrt{x^2}\ge0\forall x\)
\(\sqrt{x^2+1}>0\forall x\)
Vì thế \(\sqrt{x^2+1}+2>0\forall x\) nên không thể bằng 0 được
\(\sqrt{x^2+1}+2=0\)
\(\Leftrightarrow\sqrt{x^2+1}=-2\)
Vì \(\sqrt{x^2+1}\ge0\forall x\in R\)
Mà \(\sqrt{x^2+1}=-2\) (vô lí)
Vậy phương trình vô nghiệm.