`@` `\text {Ans}`
`\downarrow`
`16,`
`a)`
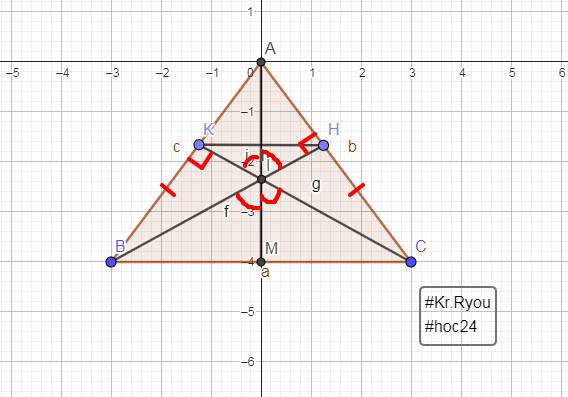
Vì `\Delta ABC` cân tại A.
`=> \text {AB = AC, }` $\widehat {B} = \widehat {C}$
Xét `\Delta BKC` và `\Delta CHB`:
$\widehat {B} = \widehat {C}$
`\text {BC chung}`
$\widehat {BKC} = \widehat {CHB} (=90^0)$
`=> \Delta BKC = \Delta CHB (ch-gn)`
`=> \text {BK = CH (2 cạnh tương ứng)}`
Ta có: \(\left\{{}\begin{matrix}\text{AB = KA + KB}\\\text{AC = HA + HC}\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}\text{AB = AC}\\\text{BK = CH}\end{matrix}\right.\)
`=> \text {HA = KA}`
Xét `\Delta AKH:`
`\text {HA = KA}`
`=> \Delta AKH` cân tại A.
`b)`
Xét `\Delta AKI` và `\Delta AHI`:
`\text {AK = AH (a)}`
`\text {AI chung}`
$\widehat {AKI} = \widehat {AHI} (=90^0)$
`=> \Delta AKI = \Delta AHI (ch-cgv)`
`=>` $\widehat {AIK} = \widehat {AIH} (\text {2 góc tương ứng})$
Mà \(\left\{{}\begin{matrix}\widehat{\text{AIK }}=\widehat{\text{CIM}}\left(\text{2 góc đối đỉnh}\right)\\\widehat{\text{AIH}}=\widehat{\text{BIM}}\left(\text{2 góc đối đỉnh}\right)\end{matrix}\right.\)
`=>`\(\widehat{\text{BIM}}=\widehat{\text{CIM}}\)
`=>` `\text {IM là phân giác của}` $\widehat {BIC}$
`c)`
`\Delta AKH` cân tại A
`=>` $\widehat {AKH} = \widehat {AHK} =$\(\dfrac{180^0-\widehat{\text{A}}}{2}\) `(1)`
`\Delta ABC` cân tại A
`=>` $\widehat {ABC} = \widehat {ACB} =$ \(\dfrac{180^0-\widehat{\text{A}}}{2}\) `(2)`
Từ `(1)` và `(2)`
`=>`\(\widehat{\text{ABC}}=\widehat{\text{AKH}}\)
Mà `2` góc này nằm ở vị trí đồng vị
`=> \text {HK // BC (t/c 2 đt' //)}.`