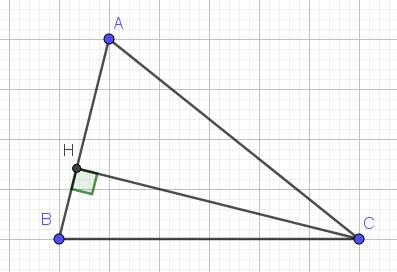
Lời giải:
a. Xét tam giác vuông $CHB$ có:
$\frac{CH}{CB}=\sin B=\sin 60^0=\frac{\sqrt{3}}{2}$
$\Rightarrow CH=\frac{\sqrt{3}}{2}CB=\frac{\sqrt{3}}{2}.12=6\sqrt{3}$ (cm)
$\widehat{A}=180^0-\widehat{B}-\widehat{C}=180^0-60^0-40^0=80^0$
Xét tam giác $AHC$ vuông có:
$\frac{CH}{CA}=\sin A$
$\Rightarrow CA=\frac{CH}{\sin A}=\frac{6\sqrt{3}}{\sin 80^0}=10,55$ (cm)
b.
$S_{ABC}=\frac{1}{2}CA.CB.\sin C=\frac{1}{2}.10,55.12\sin 40^0=40,69$ (cm2)