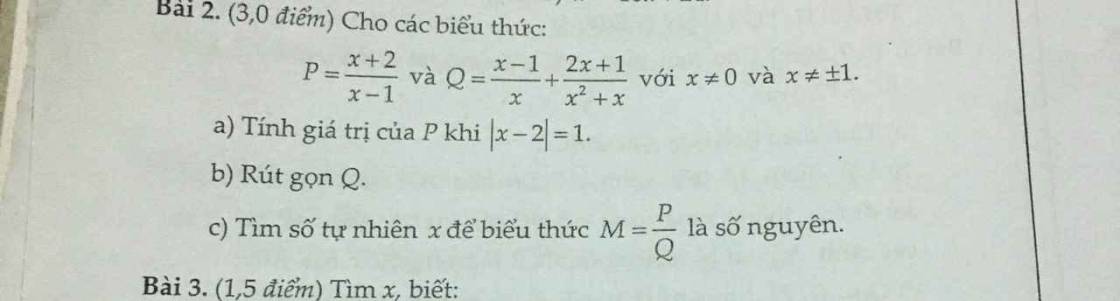Question

Answer 1

`a)|x-2|=1<=>[(x-2=1),(x-2=-1):}<=>[(x=3(t//m)),(x=1 (ko t//m)):}`

Thay `x=3` vào `P` có: `P=[3+2]/[3-1]=5/2`

`2)` Với `x \ne 0,x \ne -1` có:

`Q=[x-1]/x+[2x+1]/[x^2+x]`

`Q=[(x-1)(x+1)+2x+1]/[x(x+1)]`

`Q=[x^2-1+2x+1]/[x(x+1)]`

`Q=[x+2]/[x+1]`

`c)M=P/Q=[x+2]/[x-1]:[x+2]/[x+1]=[x+1]/[x-1]=1-2/[x-1]`

Để `M` là số nguyên thì `1-2/[x-1] in ZZ`

    `=>x-1 in Ư_2`

 Mà `Ư_2 ={+-1;+-2}`

`@x-1=1=>x=2` (t/m)

`@x-1=-1=>x=0` (ko t/m)

`@x-1=2=>x=3` (t/m)

`@x-1=-2=>x=-1` (ko t/m)