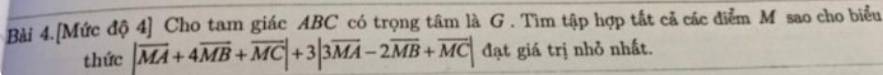(Bản chất của đoạn dưới đây là ta đi tìm các điểm cố định P, Q sao cho \(\overrightarrow{PA}+4\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow{0}\) ứng với biểu thức thứ nhất và \(3\overrightarrow{QA}-2\overrightarrow{QB}+\overrightarrow{QC}=\overrightarrow{0}\) ứng với biểu thức thứ hai)
Gọi D là trung điểm AC, P là điểm đối xứng D qua G \(\Rightarrow\overrightarrow{PD}=-2\overrightarrow{PB}\)
Hay \(\overrightarrow{PD}+2\overrightarrow{PB}=\overrightarrow{0}\)
Dựng hình bình hành ABQD \(\Rightarrow\overrightarrow{AB}=\overrightarrow{DQ}\)
Đặt \(T=\left|\overrightarrow{MA}+4\overrightarrow{MB}+\overrightarrow{MC}\right|+3\left|3\overrightarrow{MA}-2\overrightarrow{MB}+\overrightarrow{MC}\right|\)
\(=\left|2\overrightarrow{MD}+4\overrightarrow{MB}\right|+3\left|2\overrightarrow{MA}+2\overrightarrow{BM}+2\overrightarrow{MD}\right|\)
\(=2\left|\overrightarrow{MP}+\overrightarrow{PD}+2\overrightarrow{MP}+2\overrightarrow{PB}\right|+6\left|\overrightarrow{BA}+\overrightarrow{MQ}+\overrightarrow{QD}\right|\)
\(=6\left|\overrightarrow{MP}\right|+6\left|\overrightarrow{MQ}\right|=6\left(MP+MQ\right)\)
Theo BĐT tam giác ta có: \(MP+MQ\ge PQ\)
Dấu "=" xảy ra khi và chỉ khi M thuộc đoạn thẳng PQ
Vậy tập hợp M là đoạn thẳng PQ, với P và Q là các điểm được xác định như đã trình bày