a: \(A=\dfrac{\left(x-3\right)^2}{x\left(x-3\right)}=\dfrac{x-3}{x}\)
|x-5|=2
=>x-5=2 hoặc x-5=-2
=>x=3(loại) hoặc x=7(nhận)
Khi x=7 thì A=(7-3)/7=4/7
b: \(B=\left(\dfrac{-\left(x+2\right)^2+x\left(x-2\right)-4x^2-2x+4}{\left(x-2\right)\left(x+2\right)}\right):\dfrac{2x-x-3}{x\left(2-x\right)}\)
\(=\dfrac{-x^2-4x-4+x^2-2x-4x^2-2x+4}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{-x\left(x-2\right)}{x-3}\)
\(=\dfrac{-4x^2-8x}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{-x\left(x-2\right)}{x-3}\)
\(=\dfrac{-4x\left(x+2\right)}{x+2}\cdot\dfrac{-x}{x-3}=\dfrac{4x^2}{x-3}\)
c: Để A=-2 thì x-3=-2x
=>3x=3
=>x=1

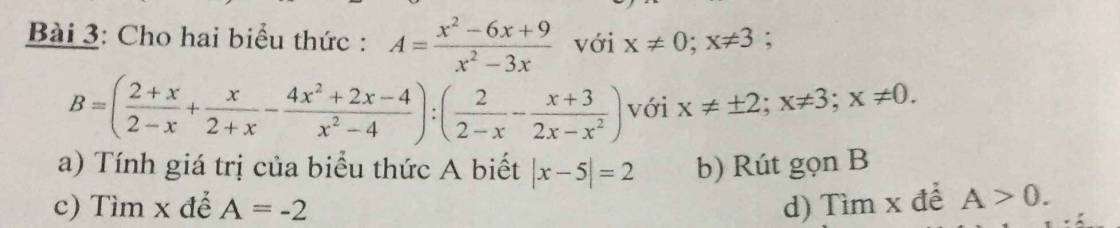













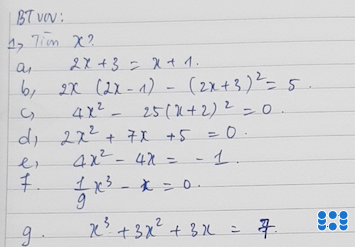

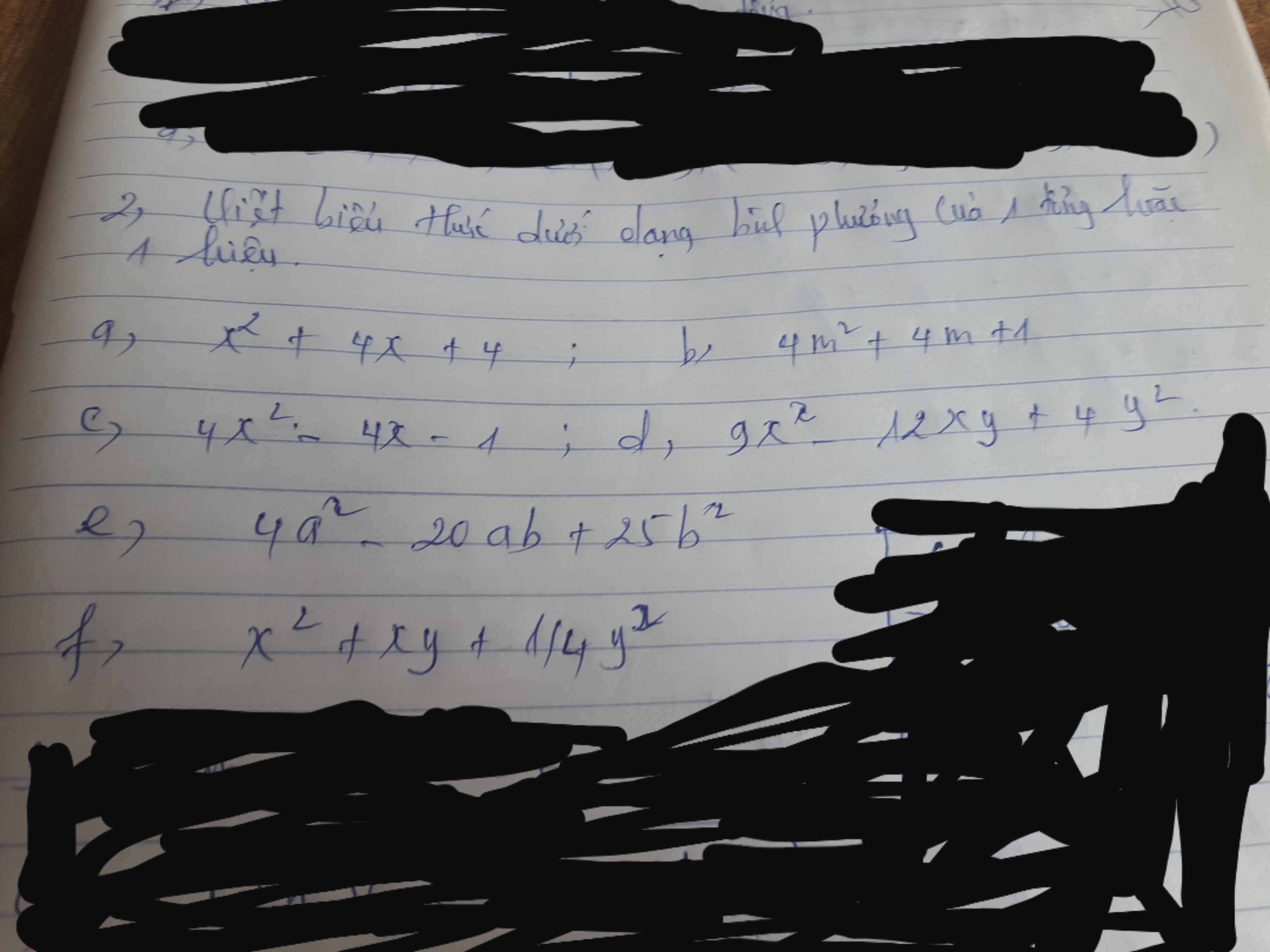



 giải thích giùm mình với
giải thích giùm mình với