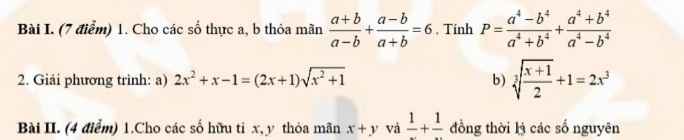1.
\(\dfrac{a+b}{a-b}+\dfrac{a-b}{a+b}=6\Rightarrow\dfrac{\left(a+b\right)^2+\left(a-b\right)^2}{a^2-b^2}=6\)
\(\Rightarrow2a^2+2b^2=6\left(a^2-b^2\right)\)
\(\Rightarrow4a^2=8b^2\Rightarrow a^2=2b^2\)
\(\Rightarrow P=\dfrac{a^4-b^4}{a^4+b^4}+\dfrac{a^4+b^4}{a^4-b^4}=\dfrac{\left(2b^2\right)^2-b^4}{\left(2b^2\right)^2+b^4}+\dfrac{\left(2b^2\right)^2+b^4}{\left(2b^2\right)^2-b^4}\)
\(=\dfrac{3b^4}{5b^4}+\dfrac{5b^4}{3b^4}=\dfrac{3}{5}+\dfrac{5}{3}=\dfrac{34}{15}\)
2.a.
\(2x^2+x-1=\left(2x+1\right)\sqrt{x^2+1}\)
\(\Leftrightarrow x^2+1-\left(2x+1\right)\sqrt{x^2+1}+x^2+x-2=0\)
Đặt \(\sqrt{x^2+1}=y>0\)
\(\Rightarrow y^2-\left(2x+1\right)y+x^2+x-2=0\)
\(\Delta=\left(2x+1\right)^2-4\left(x^2+x-2\right)=9\)
\(\Rightarrow\left[{}\begin{matrix}y=\dfrac{2x+1-3}{2}=x-1\\y=\dfrac{2x+1+3}{2}=x+2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x^2+1}=x-1\left(x\ge0\right)\\\sqrt{x^2+1}=x+2\left(x\ge-2\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2+1=x^2-2x+1\left(x\ge1\right)\\x^2+1=x^2+4x+4\left(x\ge-2\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=-\dfrac{3}{4}\left(tm\right)\end{matrix}\right.\)
2b.
Đặt \(\sqrt[3]{\dfrac{x+1}{2}}=y\Rightarrow\dfrac{x+1}{2}=y^3\Rightarrow x+1=2y^3\)
Ta được hệ:
\(\left\{{}\begin{matrix}y+1=2x^3\\x+1=2y^3\end{matrix}\right.\)
Trừ vế cho vế:
\(\Rightarrow2x^3-2y^3=y-x\)
\(\Leftrightarrow\left(x-y\right)\left(2x^2-2xy+2y^2+1\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left[\left(x-y\right)^2+x^2+y^2+1\right]=0\)
\(\Leftrightarrow x=y\)
\(\Rightarrow\sqrt[3]{\dfrac{x+1}{2}}=x\)
\(\Leftrightarrow2x^3-x-1=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x^2+2x+1\right)=0\)
\(\Leftrightarrow x=1\)