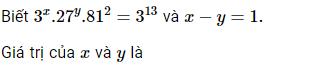Question

Answer 1

\(\Leftrightarrow3^x\cdot3^{3y}\cdot3^8=3^{13}\)

=>x+3y=5

mà x-y=1

nên 4y=4

=>y=1

=>x=2

Answer 2

\(x-y=1\\=>x=1+y\\ 3^x.3^{3y}.3^8=3^{13}\\ 3^{x+3y+8}=3^{13}\\ x+3y+8=13\\ x+3y=5\\ 1+y+3y=5\\ 1+4y=5\\ 4y=4\\ y=1=>x=1+1\\ x=2\)

Answer 3

\(3^x\cdot27^y\cdot81^2=3^{13}\\ \Leftrightarrow3^x\cdot3^{3y}\cdot3^8=3^{13}\\ \Leftrightarrow3^{x+3y+8}=3^{13}\\ \Leftrightarrow x+3y+8=13\\ \Leftrightarrow x+3y=5\\ \Rightarrow x+3y-x+y=5-1=4\Leftrightarrow4y=4\Leftrightarrow y=1\\ \Rightarrow x=2\)

Answer 4

⇔3x⋅33y⋅38=313⇔3x⋅33y⋅38=313

=>x+3y=5

mà x-y=1

nên 4y=4

=>y=1

=>x=2