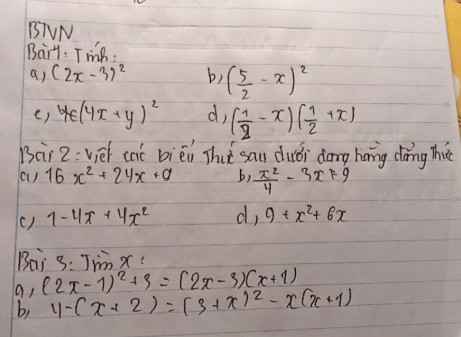Bài 1
a) \(\left(2x-3\right)^2=\left(2x\right)^2-2.2x.3+3^2=4x^2-12x+9\)
b) \(\left(\dfrac{5}{2}-x\right)^2=\left(\dfrac{5}{2}\right)^2-2.\dfrac{5}{2}.x+x^2=\dfrac{25}{4}-5x+x^2\)
c) \(\left(4x+4\right)^2=\left(4x\right)^2+2.4x.4+4^2=16x^2+32x+16\)
d) \(\left(\dfrac{1}{2}-x\right)\left(\dfrac{1}{2}+x\right)=\left(\dfrac{1}{2}\right)^2-x^2\)
Bài 2 :
a) \(16x^2+24x+9=\left(4x\right)^2+2.4x.3+3^2=\left(4x+3\right)^2\)
b) \(\dfrac{x^2}{4}-3x+9=\left(\dfrac{x}{2}\right)^2-2.\dfrac{x}{2}.3+3^2=\left(\dfrac{x}{2}-3\right)^2\)
c) \(1-4x+4x^2=1^2-2.1.2x+\left(2x\right)^2=\left(1-2x\right)^2\)
d) \(9+x^2+6x=x^2+6x+9=x^2+2.x.3+3^2=\left(x+3\right)^2\)
B3:
a. \(\left(2x-1\right)^2+3=\left(2x-3\right)\left(x+1\right)\)
\(\Leftrightarrow\left(2x\right)^2-2.2x.1+1+3=2x^2-x-3\)
\(\Leftrightarrow4x^2-4x+4-2x^2+x+3=0\)
\(\Leftrightarrow2x^2-3x+7=0\)
pt có các số hữu tỉ lẻ
=> vô nghiệm
b.
\(4-\left(x+2\right)=\left(3+x\right)^2-x\left(x+1\right)\)
\(\Leftrightarrow4-x-2=3^2+2.3.x+x^2-x^2-x\)
\(\Leftrightarrow2-x=9+6x-x\)
\(\Leftrightarrow2-x-9-6x+x=0\)
\(\Leftrightarrow-7-6x=0\)
\(\Rightarrow6x=-7-0=-7\)
\(\Rightarrow x=\dfrac{-7}{6}\)