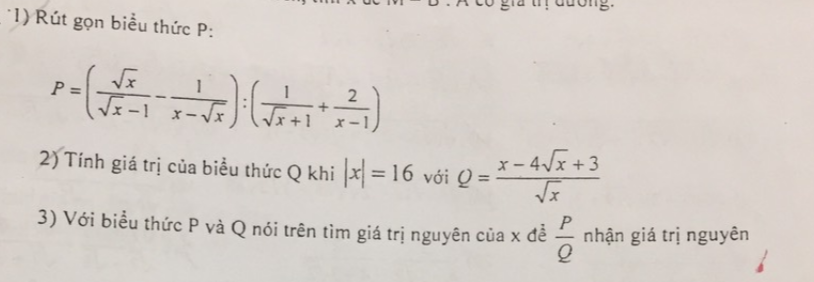ĐK: \(\sqrt{x}>0\)
\(P=\dfrac{\sqrt{x}.\sqrt{x}-1}{x-\sqrt{x}}:\left(\dfrac{\sqrt{x}-1+2}{x-1}\right)\)
\(=\dfrac{x-1}{x-\sqrt{x}}.\dfrac{x-1}{\sqrt{x}+1}\)
\(=\dfrac{\left(x-1\right)^2}{\left(x-1\right).\sqrt{x}}=\dfrac{x-1}{\sqrt{x}}\)
1: \(P=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}-1+2}{x-1}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}}\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+1}=\dfrac{x-1}{\sqrt{x}}\)
2: |x|=16
nên x=16(nhận) hoặc x=-16(loại)
Khi x=16 thì \(A=\dfrac{16-4\cdot4+3}{4}=\dfrac{3}{4}\)
3: \(\dfrac{P}{Q}=\dfrac{x-1}{\sqrt{x}}:\dfrac{x-4\sqrt{x}+3}{\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
Để P/Q là số nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{4;2;5;1;7\right\}\)
hay \(x\in\left\{16;4;25;49\right\}\)