Giải thích:
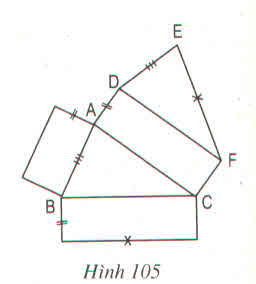
Hạ BE⊥DC (E thuộc DC).
Tứ giác ABED có: \(\left\{{}\begin{matrix}\widehat{DAB}=\widehat{ADE}=\widehat{BED}=90^0\\AD=AB\end{matrix}\right.\)
\(\Rightarrow\)ABED là hình vuông.
\(\Rightarrow DE=AB=\dfrac{DC}{2};\widehat{BDC}=45^0\) \(\Rightarrow\)E là trung điểm DC.
△BCD có: BE vừa là trung tuyến vừa là đường cao.
\(\Rightarrow\)△BCD cân tại B.
Mà \(\widehat{BDC}=45^0\Rightarrow\)△BCD vuông cân tại B.
\(\Rightarrow BC=BD=a\sqrt{2};DC=BC\sqrt{2}=a\sqrt{2}.\sqrt{2}=2a\)
\(\Rightarrow AB=BE=a\)
\(S_{ABCD}=\dfrac{\left(AB+CD\right).BE}{2}=\dfrac{\left(a+2a\right).a}{2}=\dfrac{3a^2}{2}\)
Đúng 2
Bình luận (0)
