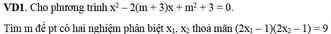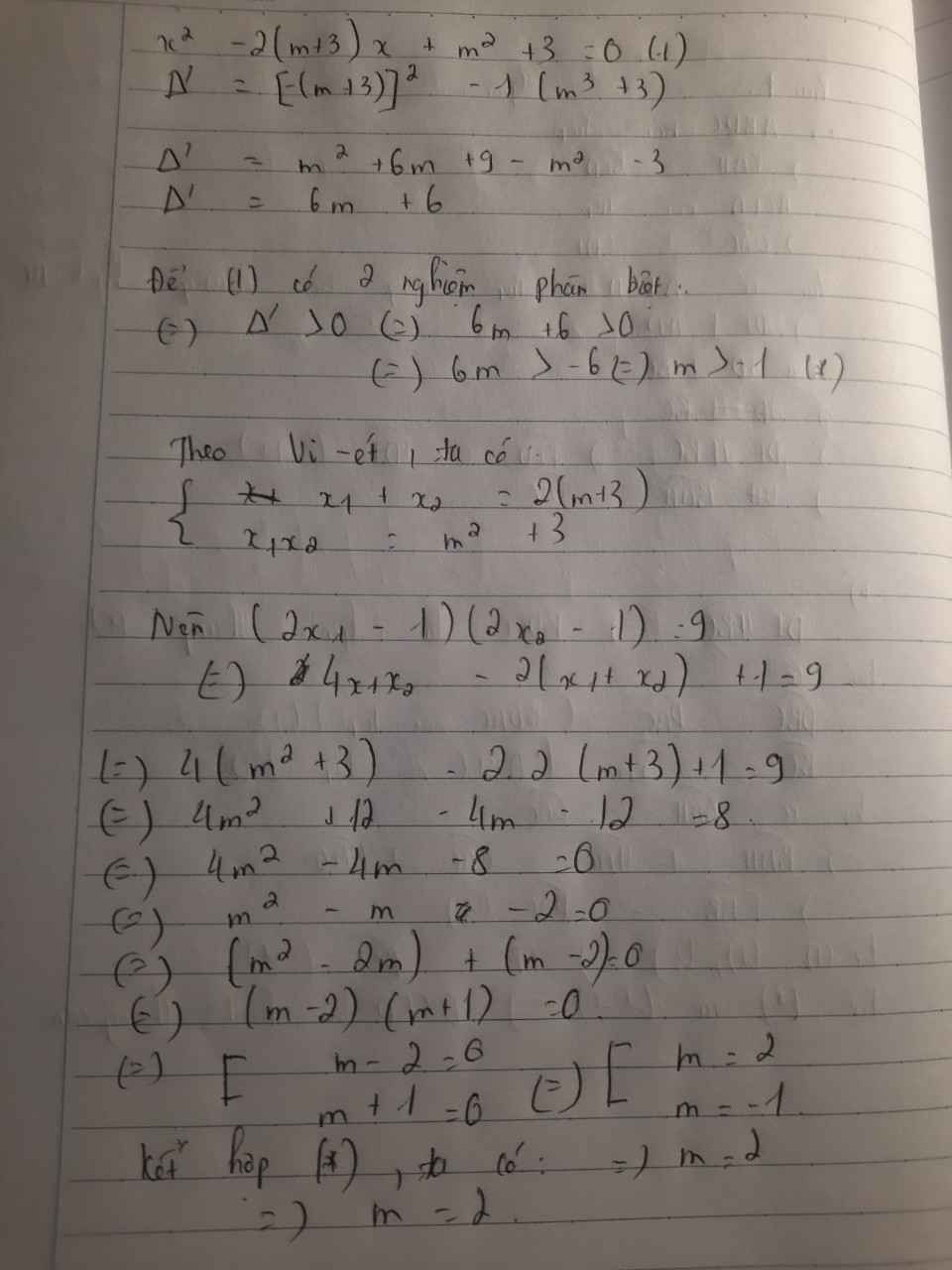Để pt có 2 nghiệm phân biệt thì \(\Delta'>0\)
\(\Leftrightarrow\left[-\left(m+3\right)\right]^2-\left(m^2+3\right)>0\\ \Leftrightarrow m^2+6m+9-m^2-3>0\\ \Leftrightarrow6m+6>0\\ \Leftrightarrow m>-1\)
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m+6\\x_1x_2=m^2+3\end{matrix}\right.\)
\(\left(2x_1-1\right)\left(2x_2-1\right)=9\\ \Leftrightarrow4x_1x_2-2x_2-2x_1+1-9=0\\ \Leftrightarrow4\left(m^2+3\right)-2\left(x_1+x_2\right)-8=0\\ \Leftrightarrow4m^2+12-2\left(2m+6\right)-8=0\\ \Leftrightarrow4m^2+12-4m-12-8=0\\ \Leftrightarrow4m^2-4m-8=0\\ \Leftrightarrow m^2-m-2=0\\ \Leftrightarrow\left(m+1\right)\left(m-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-1\left(ktm\right)\\m=2\left(tm\right)\end{matrix}\right.\)