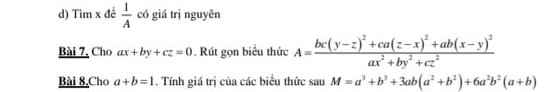Question

Answer 1

Bài 8:

\(M=a^3+b^3+3ab\left(a^2+b^2\right)+6a^2b^2\left(a+b\right)\)

\(=\left(a+b\right)\left(a^2-ab+b^2\right)+3ab\left(1-2ab\right)+6a^2b^2\)

\(=a^2-ab+b^2+3ab-6a^2b^2+6a^2b^2\)

\(=a^2+2ab+b^2=\left(a+b\right)^2=1\)

Answer 2

Bài 8:

\(M=\left(a+b\right)^3-3ab\left(a+b\right)+3ab\left[\left(a+b\right)^2-2ab\right]+6a^2b^2\cdot1\)

\(=1^3-3ab+3ab\cdot1-3ab\cdot2ab+6a^2b^2=1\)