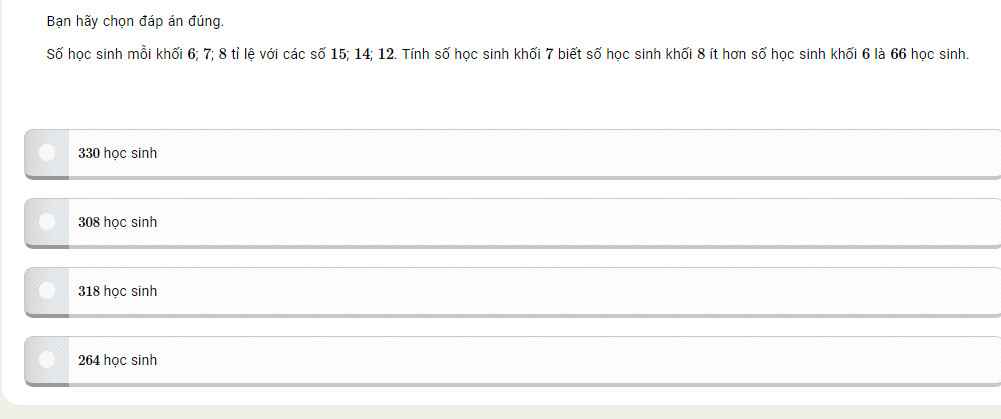
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{15}=\dfrac{b}{14}=\dfrac{c}{12}=\dfrac{a-c}{15-12}=\dfrac{66}{3}=22\)
Do đó: a=330; b=308; c=264
Vậy: Chọn B
Gọi hs khối 6;7;8 lần lượt là a ; b ; c ( a ; b; c thuộc N*)
Theo bài ra áp dụng dãy tỉ số bằng nhau
\(\dfrac{a}{15}=\dfrac{b}{14}=\dfrac{c}{12}=\dfrac{a-c}{15-12}=\dfrac{66}{3}=22\Rightarrow b=308\)(tm)
-> chọn B
Gọi số học sinh mỗi khối \(6;7;8\) lần lượt là \(x,y,z\) (\(x,y,z\) nguyên dương)
Ta có: \(\dfrac{x}{15}=\dfrac{y}{14}=\dfrac{z}{12};x-y=66\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{15}-\dfrac{y}{14}=\dfrac{z}{12}=\dfrac{x-z}{15-12}=\dfrac{66}{3}=22\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{15}=22\Leftrightarrow x=330\\\dfrac{y}{14}=22\Leftrightarrow y=308\\\dfrac{z}{12}=22\Leftrightarrow z=264\end{matrix}\right.\)
Vậy số học sinh khối \(7\) là \(308\) học sinh.
Gọi số học sinh khối 6,7,8 lần lượt là a,b,c (a,b,c:nguyên,dương)
Theo các dữ kiện đề bài, ta có:
\(\dfrac{a}{15}=\dfrac{b}{14}=\dfrac{c}{12}=\dfrac{a-c}{15-12}=\dfrac{66}{3}=22\\ \Rightarrow\left\{{}\begin{matrix}a=22.15=330\\b=22.14=308\\c=22.12=264\end{matrix}\right.\)
=> Số học sinh khối 7: 308(học sinh)
Gọi số học sinh của các khối 6 ; 7 ; 8 lần lượt là x ; y ; z ( x ; y ; z khác 0 ) .
Theo đề ta có : x : y : z = 15 : 14 ; 12 và x - z = 66
→ \(\dfrac{x}{15} = \dfrac{y}{14} = \dfrac{z}{12}\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\dfrac{x}{15} = \dfrac{y}{14} = \dfrac{z}{12} = \dfrac{x - z }{15 - 12 } = \dfrac{66}{3} = 22\)
Từ đây suy ra :
\(\dfrac{x}{15} = 22 \) → x = 330
\(\dfrac{y}{14} = 22 \) → y = 308
\(\dfrac{z}{12} = 22 \) → z = 264
Vậy số học sinh của các khối 6 ; 7 ; 8 lần lượt là 330 ; 308 ; 264 học sinh
→ B