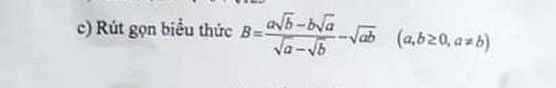Question

Answer 1

\(B=\dfrac{\sqrt {ab}(\sqrt a - \sqrt b)}{\sqrt a-\sqrt b}-\sqrt{ab} =\sqrt{ab}-\sqrt{ab}=0\)

Answer 2

\(\dfrac{a\sqrt{b}-b\sqrt{a}}{\sqrt{a}-\sqrt{b}}-\sqrt{ab}=\dfrac{\sqrt{ab}\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}-\sqrt{ab}=\sqrt{ab}-\sqrt{ab}=0\)

Answer 3

\(\dfrac{a\sqrt{b}-b\sqrt{a}-\sqrt{ab}.\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}=\dfrac{a\sqrt{b}-b\sqrt{a}-a\sqrt{b}+b\sqrt{a}}{\sqrt{a}-\sqrt{b}}=0\text{ }\)