\(a,2x\left(2y+1\right)-6y-3=2x\left(2y+1\right)-\left(6y+3\right)=2x\left(2y+1\right)-3\left(2y+1\right)=\left(2y+1\right)\left(2x-3\right)\\ b,x^2-6x+8=\left(x^2-2x\right)-\left(4x-8\right)=x\left(x-2\right)-4\left(x-2\right)=\left(x-2\right)\left(x-4\right)\\ c,x^3-y^3+x^2y-xy^2=\left(x-y\right)\left(x^2+xy+y^2\right)+xy\left(x-y\right)=\left(x-y\right)\left(x^2+xy+y^2+xy\right)=\left(x-y\right)\left(x^2+2xy+y^2\right)=\left(x-y\right)\left(x+y\right)^2\)
\(d,\left(x^2-2x\right)^2-2\left(x^2-2x\right)-3=\left[\left(x^2-2x\right)^2-3\left(x^2-2x\right)\right]+\left[\left(x^2-2x\right)-3\right]=\left(x^2-2x\right)\left(x^2-2x-3\right)+\left(x^2-2x-3\right)=\left(x^2-2x-3\right)\left(x^2-2x+1\right)=\left[\left(x^2-3x\right)+\left(x-3\right)\right]\left(x-1\right)^2=\left[x\left(x-3\right)+\left(x-3\right)\right]\left(x-1\right)^2=\left(x+1\right)\left(x-3\right)\left(x-1\right)^2\)
a) \(2x\left(2y+1\right)-6y-3=2x\left(2y+1\right)-3\left(2y+1\right)=\left(2x-3\right)\left(2y+1\right).\)
b) \(x^2-6x+8=x^2-6x+9-1=\left(x-3\right)^2-1=\left(x-3-1\right)\left(x-3+1\right)=\left(x-4\right)\left(x-2\right).\)
c) \(x^3-y^3+x^2y-xy^2=\left(x-y\right)\left(x^2+xy+y^2\right)+xy\left(x-y\right)=\left(x-y\right)\left(x^2+y^2+2xy\right)=\left(x-y\right)\left(x+y\right)^2.\)
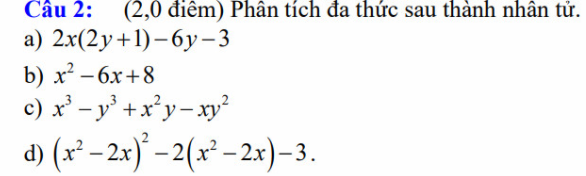
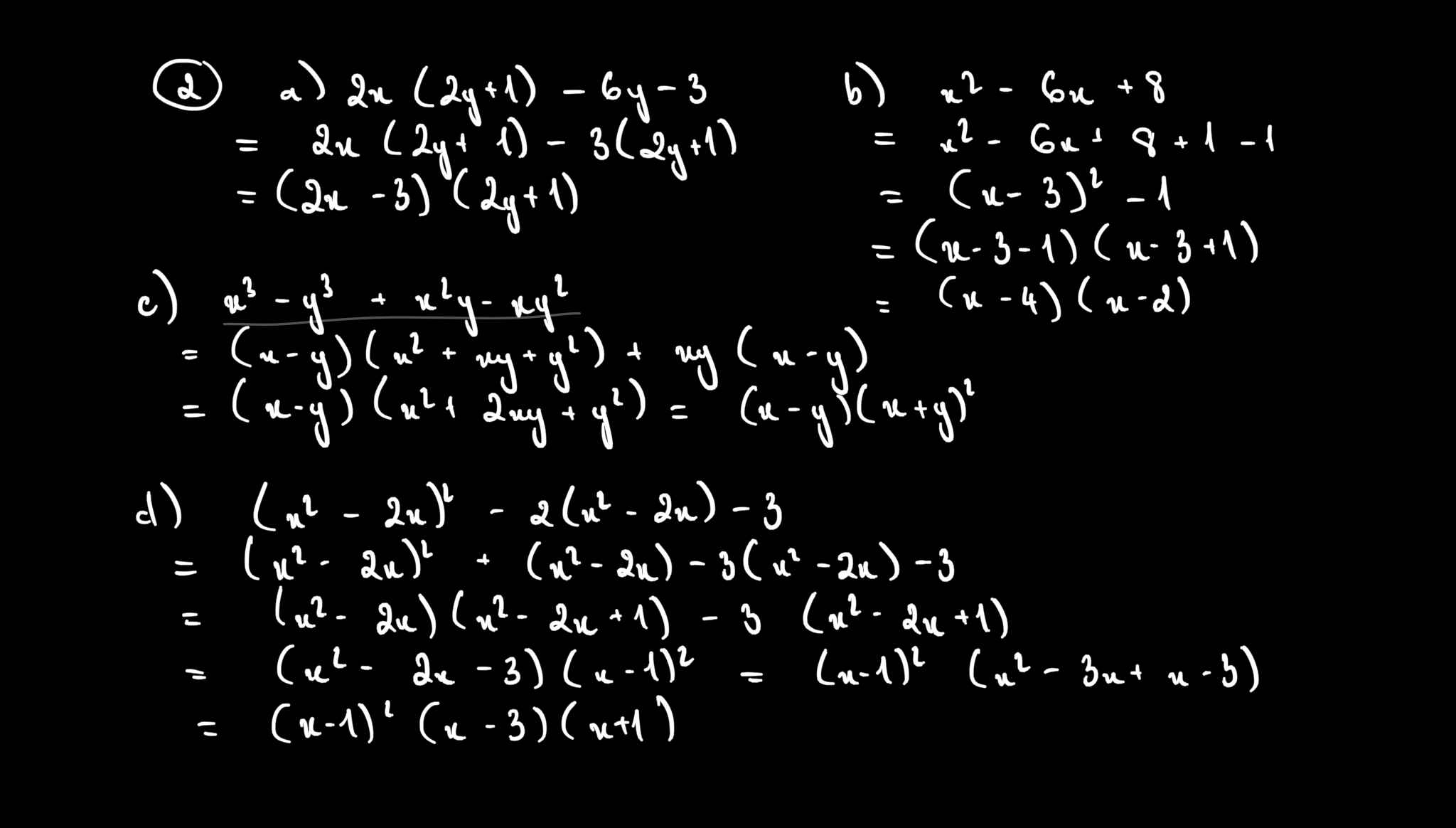
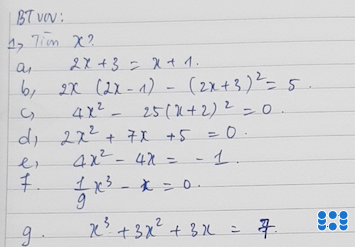
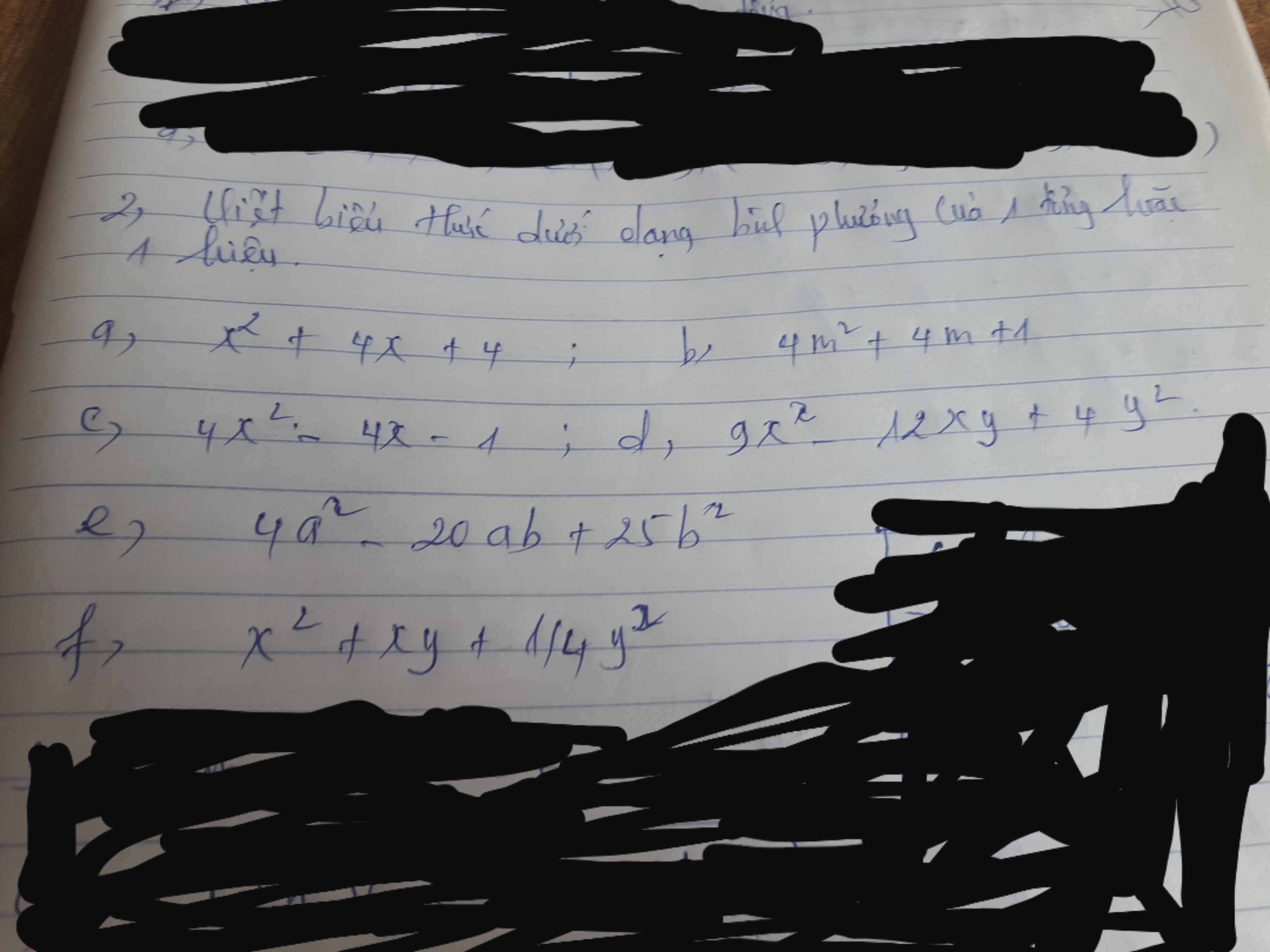
giải thích giùm mình với