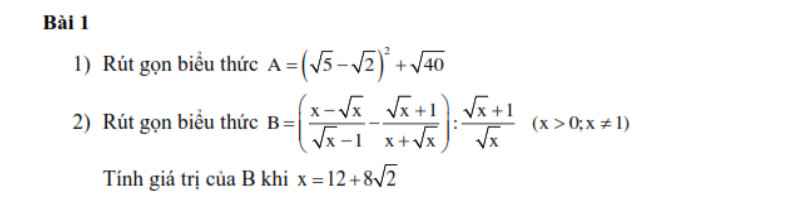1: \(A=7-2\sqrt{10}+2\sqrt{10}=7\)
\(1,A=7-2\sqrt{10}+2\sqrt{10}=7\\ 2,B=\left[\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}-\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\right]\cdot\dfrac{\sqrt{x}}{\sqrt{x}+1}\\ B=\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)\cdot\dfrac{\sqrt{x}}{\sqrt{x}+1}=\dfrac{\sqrt{x}-1}{\sqrt{x}}\cdot\dfrac{\sqrt{x}}{\sqrt{x}+1}=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\\ x=12+8\sqrt{2}=\left(2\sqrt{2}+2\right)^2\\ \Leftrightarrow B=\dfrac{2\sqrt{2}+2-1}{2\sqrt{2}+2+1}=\dfrac{2\sqrt{2}+1}{2\sqrt{2}+3}=\dfrac{\left(2\sqrt{2}+1\right)\left(3-2\sqrt{2}\right)}{9-8}\\ B=6\sqrt{2}-8+3-2\sqrt{2}=4\sqrt{2}-5\)