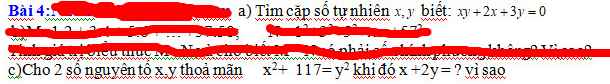Question

Answer 1

giúp mình với

Answer 2

\(x^2+117=y^2\)

Do x,y nguyên tố và  \(y^2>117>2\) nên y lẻ

Do đó x chẵn

Mà x nguyên tố nên \(x=2\Rightarrow y^2=117+4=121\Rightarrow y=11\)

Vậy \(x+2y=2+2\cdot11=2+22=24\)

Answer 3

\(xy+2x+3y=0\\ \Rightarrow xy+2x+3y+6=6\\ \Rightarrow x\left(y+2\right)+3\left(y+2\right)=6\\ \Rightarrow\left(x+3\right)\left(y+2\right)=6=1\cdot6=2\cdot3\)

Từ đó bạn liệt kê các trường hợp ra