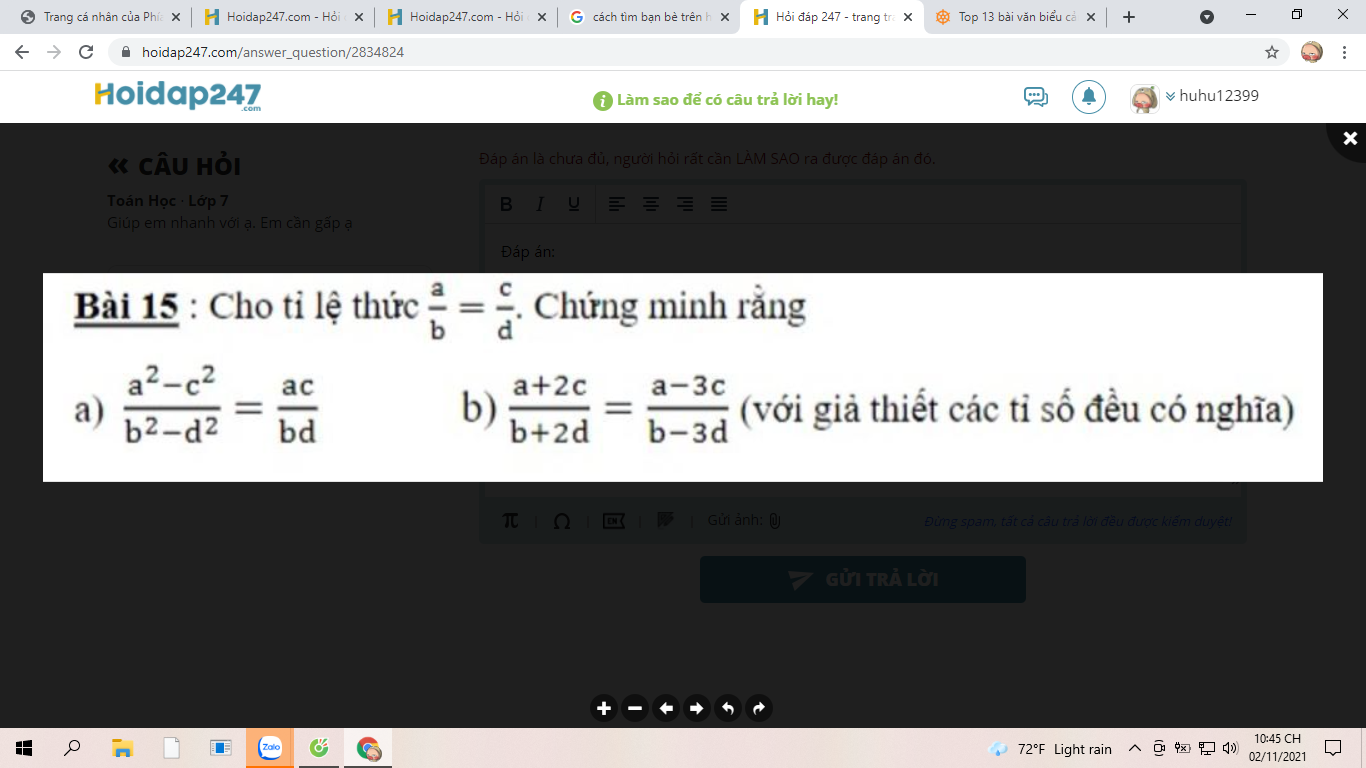
a: Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
\(\dfrac{a^2-c^2}{b^2-d^2}=\dfrac{b^2k^2-d^2k^2}{b^2-d^2}=k^2\)
\(\dfrac{ac}{bd}=\dfrac{bk\cdot dk}{bd}=k^2\)
Do đó: \(\dfrac{a^2-c^2}{b^2-d^2}=\dfrac{ac}{bd}\)
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Leftrightarrow a=bk;c=dk\)
\(a,VT=\dfrac{b^2k^2-d^2k^2}{b^2-d^2}=k^2\\ VP=\dfrac{bk\cdot dk}{bd}=k^2\\ \Leftrightarrow VT=VP\)
\(b,\) Áp dụng tc dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{2c}{2d}=\dfrac{3c}{3d}=\dfrac{a+2c}{b+2d}=\dfrac{a-3c}{b-3d}\)