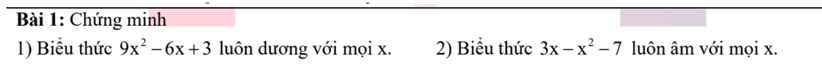1) \(9x^2-6x+3=\left(9x^2-6x+1\right)+2=\left(3x-1\right)^2+2\ge2>0\forall x\)
2) \(3x-x^2-7=-\left(x^2-3x+\dfrac{9}{4}\right)-\dfrac{19}{4}=-\left(x-\dfrac{3}{2}\right)^2-\dfrac{19}{4}\le-\dfrac{19}{4}< 0\forall x\)
1: \(9x^2-6x+3\)
\(=9x^2-6x+1+2\)
\(=\left(3x-1\right)^2+2>0\forall x\)
2: \(-x^2+3x-7\)
\(=-\left(x^2-3x+7\right)\)
\(=-\left(x^2-3x+\dfrac{9}{4}+\dfrac{19}{4}\right)\)
\(=-\left(x-\dfrac{3}{2}\right)^2-\dfrac{19}{4}< 0\forall x\)