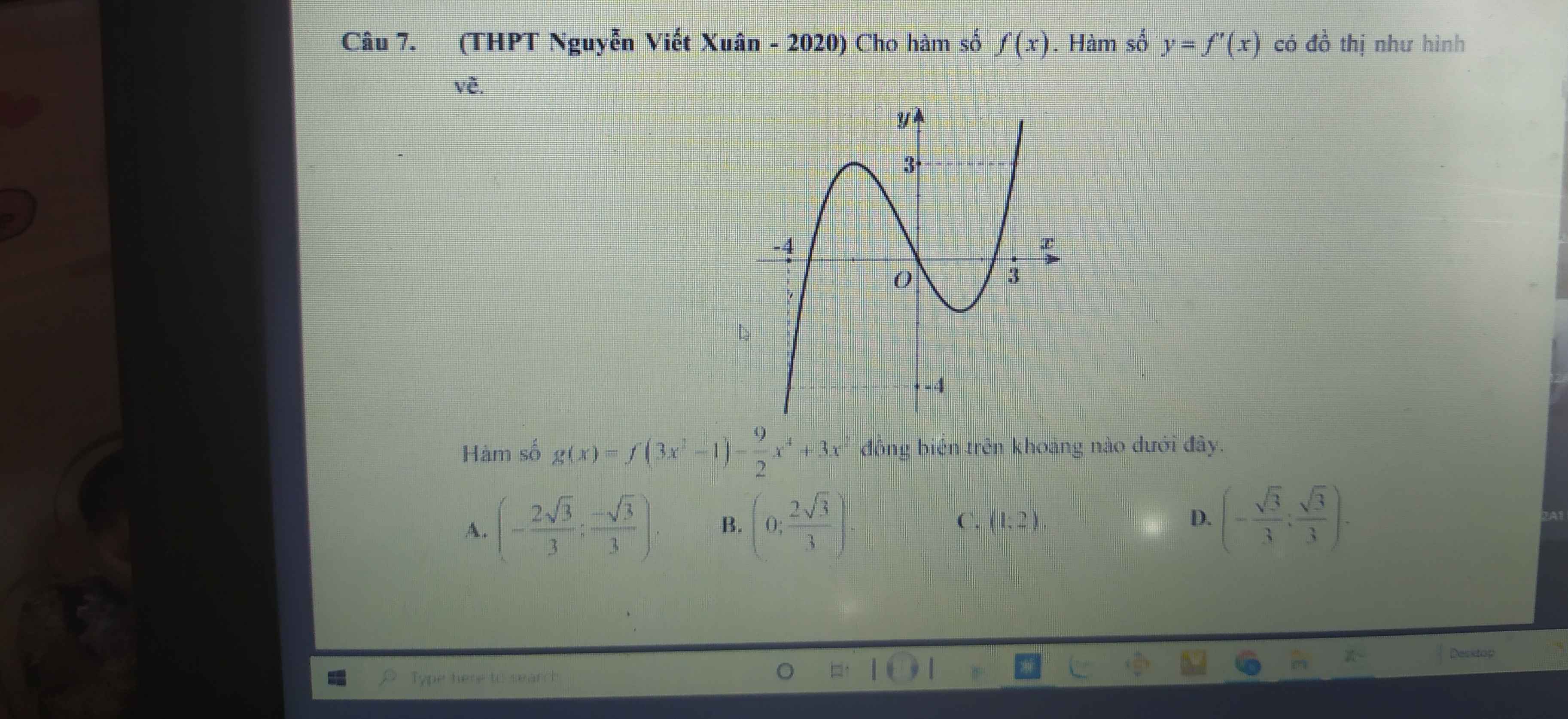
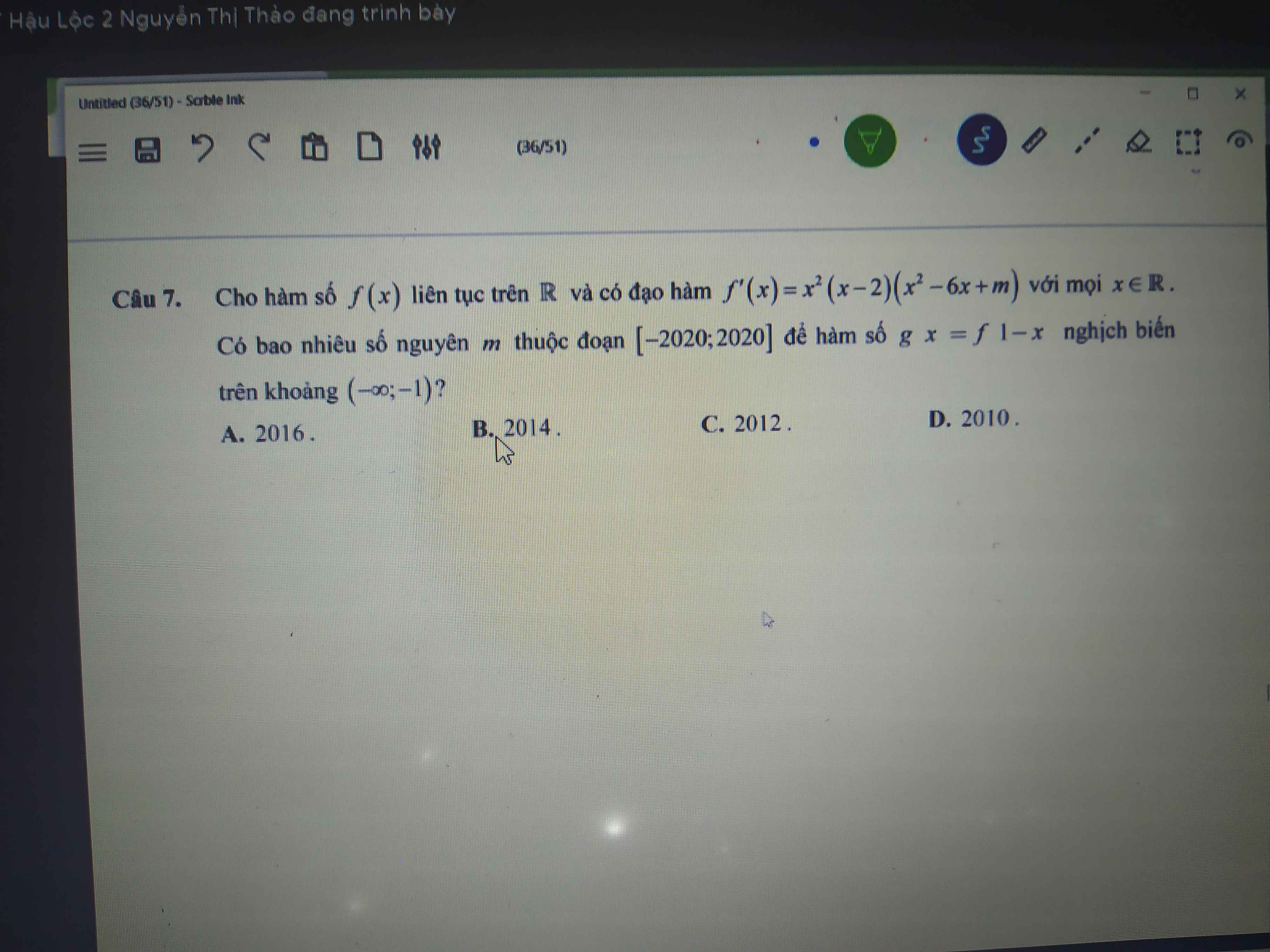
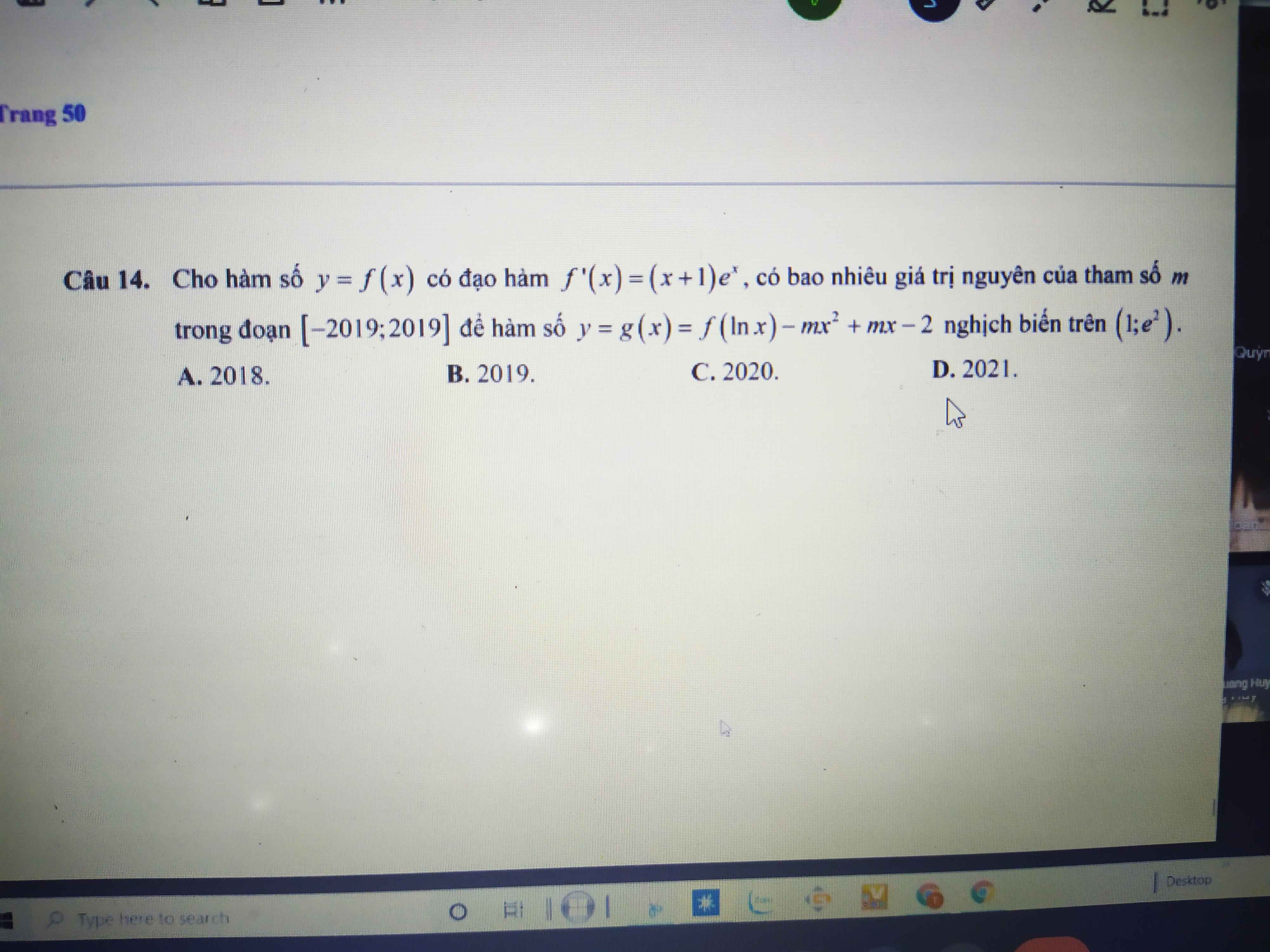
\(g'\left(x\right)=6x.f'\left(3x^2-1\right)-18x^3+6x=6x\left[f'\left(3x^2-1\right)-\left(3x^2-1\right)\right]\)
\(g'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\f'\left(3x^2-1\right)=3x^2-1\end{matrix}\right.\)
Từ đồ thị ta thấy \(f'\left(3x^2-1\right)\) cắt \(y=3x^2-1\) tại 3 điểm: \(\left[{}\begin{matrix}3x^2-1=-4\left(vn\right)\\3x^2-1=0\\3x^2-1=3\end{matrix}\right.\)
\(\Rightarrow x=\left\{-\dfrac{2\sqrt{3}}{3};-\dfrac{\sqrt{3}}{3};\dfrac{\sqrt{3}}{3};\dfrac{2\sqrt{3}}{3}\right\}\) (theo thứ tự là a;b;c;d)
BBT:
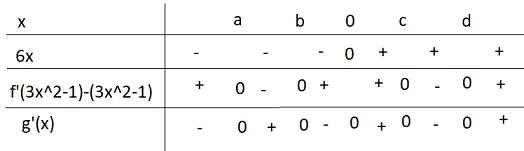
A đúng
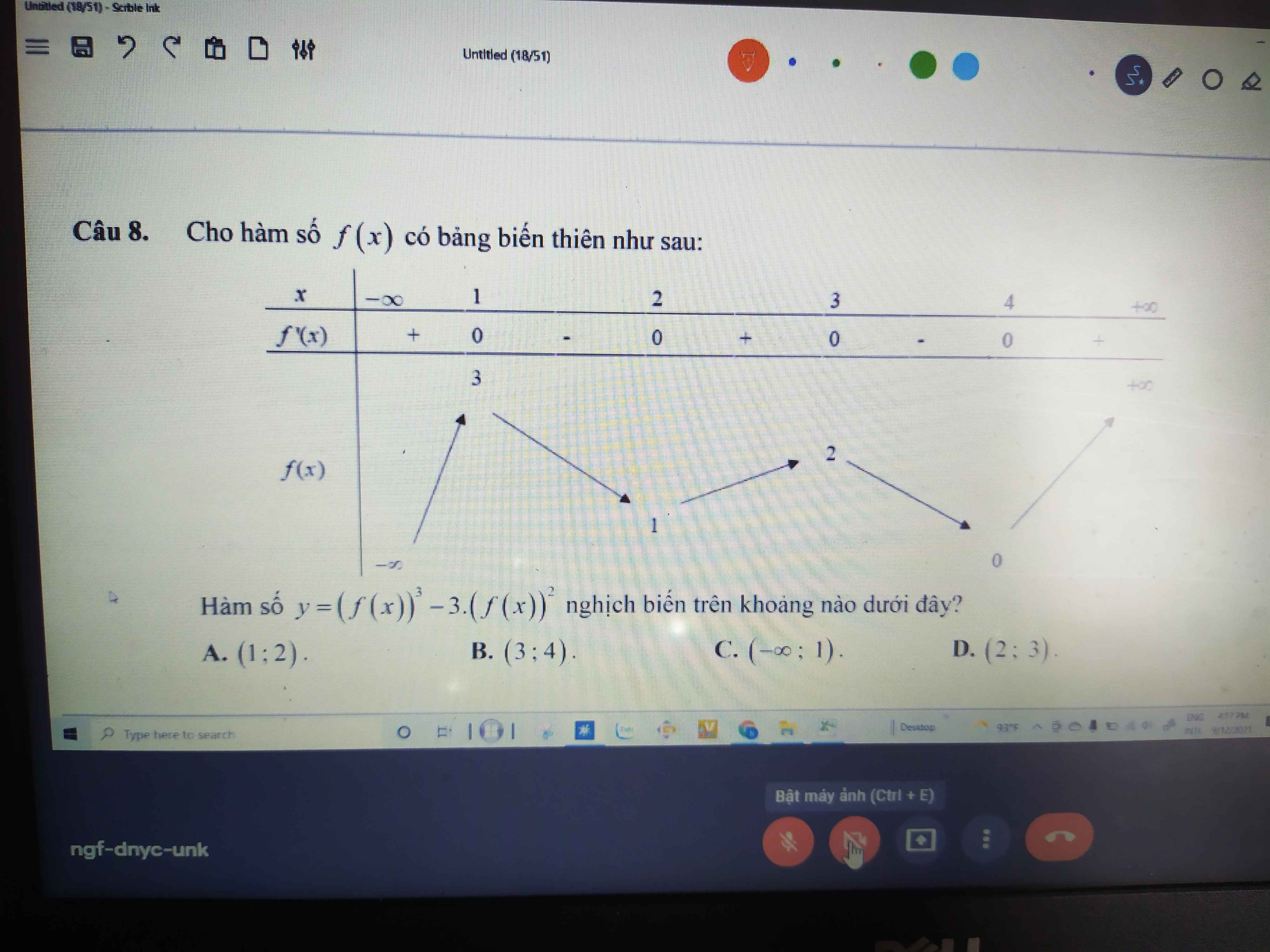
\(y'=3f'\left(x\right).f\left(x\right).\left[f\left(x\right)-2\right]\)
Làm biếng kẻ BBT nên nhận xét nhanh:
\(f\left(x\right)=0\) có 1 nghiệm bội chẵn 4 và 1 nghiệm nhỏ hơn 1 \(\Rightarrow\) trên \(\left(-\infty;1\right)\) thì \(y'\) chắc chắn đổi dấu => loại C. Đồng thời trên (2;3), (3;4) thì \(f\left(x\right)\) dương
\(f\left(x\right)-2=0\) có nghiệm bội chẵn 3, 1 nghiệm lớn hơn 4, 1 nghiệm giữa 1 và 2 (loại A), đồng thời trên (2;3), (3;4) thì \(f\left(x\right)-2\) đều âm
\(\Rightarrow f\left(x\right).\left[f\left(x\right)-2\right]\) âm trên (2;3); (3;4)
\(\Rightarrow\left(2;3\right)\) là đáp án đúng