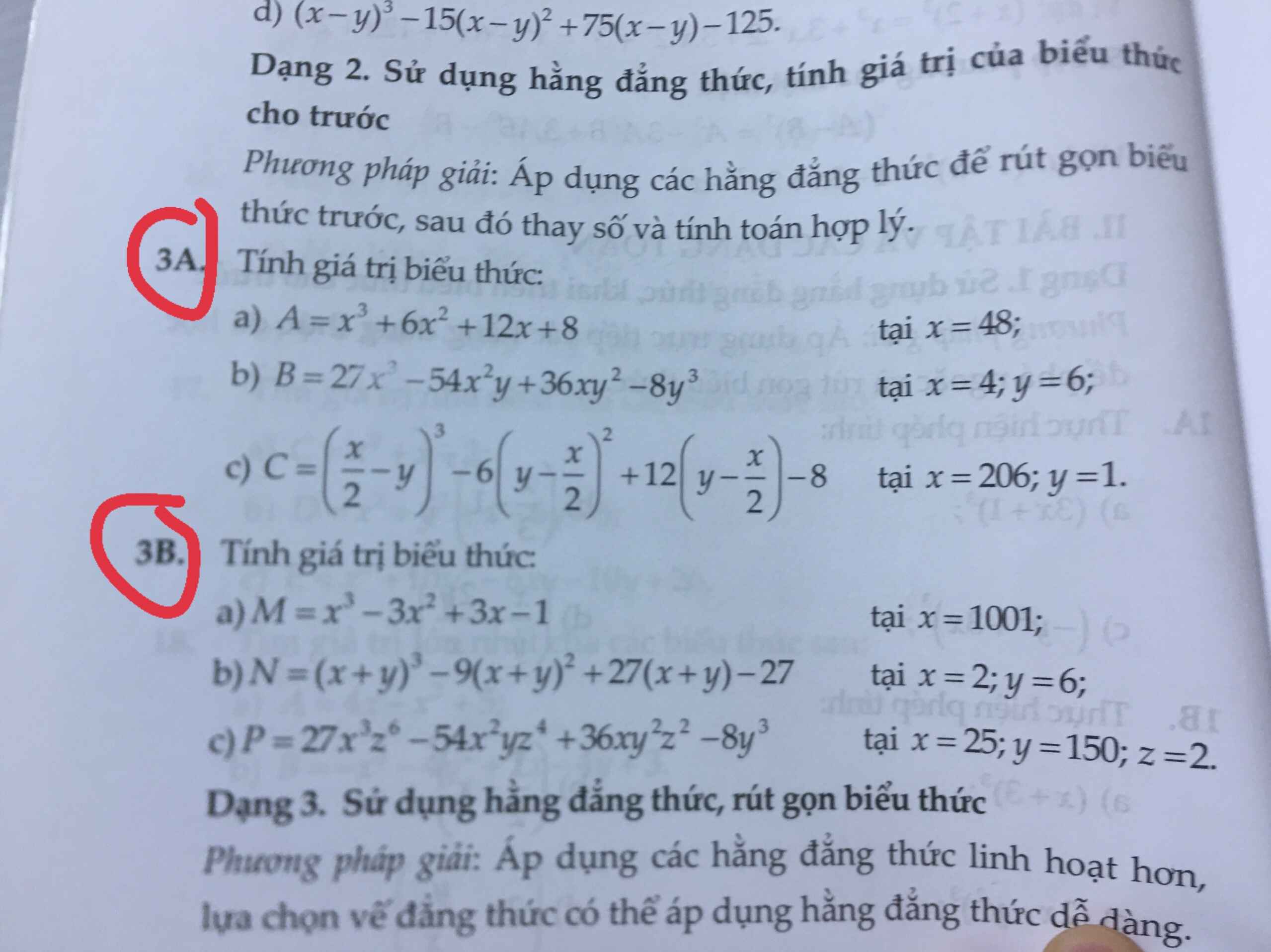3B:
a: Ta có: \(M=x^3-3x^2+3x-1\)
\(=\left(x-1\right)^3\)
\(=\left(1001-1\right)^3\)
\(=1000^3=1000000000\)
b: Ta có: \(N=\left(x+y\right)^3-9\left(x+y\right)^2+27\left(x+y\right)-27\)
\(=\left(x+y-3\right)^3\)
\(=\left(2+6-3\right)^3\)
\(=5^3=125\)
c: Ta có: \(P=27x^3z^6-54x^2yz^4+36xy^2z^2-8y^3\)
\(=\left(3xz^2-2y\right)^3\)
\(=\left(3\cdot25\cdot2^2-2\cdot150\right)^3\)
\(=0^3=0\)
3A:
a: Ta có: \(A=x^3+6x^2+12x+8\)
\(=\left(x+2\right)^3\)
\(=50^3=125000\)
b: Ta có: \(B=27x^3-54x^2y+36xy^2-8y^3\)
\(=\left(3x-2y\right)^3\)
\(=\left(3\cdot4-2\cdot6\right)^3\)
=0
c: Ta có: \(C=\left(\dfrac{x}{2}-y\right)^3-6\left(y-\dfrac{x}{2}\right)^2+12\left(y-\dfrac{x}{2}\right)-8\)
\(=\left(\dfrac{1}{2}x-y-2\right)^3\)
\(=\left(\dfrac{1}{2}\cdot206-1-2\right)^3\)
\(=100^3=1000000\)
Bài 3A.
a.
\(A=x^3+6x^2+12x+8=x^3+3x^2.2+3.x.2^2+2^3=(x+2)^3\)
\(=(48+2)^3=125000\)
b.
\(B=27x^3-54x^2y+36xy^2-8y^3\)
\(=(3x)^3-3.(3x)^2.2y+3.3x.(2y)^2-(2y)^3\)
\(=(3x-2y)^3=(3.4-2.6)^3=0\)
c.
\(C=(\frac{x}{2}-y)^3-3.2(\frac{x}{2}-y)^2+3.2^2(\frac{x}{2}-y)-2^3+24(y-\frac{x}{2})\)
\(=(\frac{x}{2}-y-2)^3+24(y-\frac{x}{2})=(103-1-2)^3+24(1-103)\)
\(=100^3-2448=997552\)