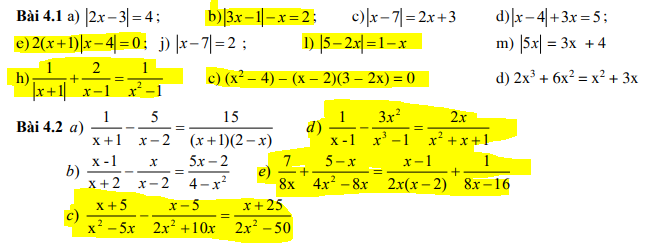Bài 4.1:
b: Ta có: \(\left|3x-1\right|-x=2\)
\(\Leftrightarrow\left|3x-1\right|=x+2\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=x+2\left(x\ge\dfrac{1}{3}\right)\\1-3x=x+2\left(x< \dfrac{1}{3}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=3\\-4x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\left(nhận\right)\\x=\dfrac{-1}{4}\left(nhận\right)\end{matrix}\right.\)
e: Ta có: \(2\left(x+1\right)\left|x-4\right|=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=4\end{matrix}\right.\)
i: Ta có: \(\left|5-2x\right|=1-x\)
\(\Leftrightarrow\left[{}\begin{matrix}5-2x=1-x\left(x\le\dfrac{5}{2}\right)\\5-2x=x-1\left(x>\dfrac{5}{2}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-x=-4\\-3x=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\left(loại\right)\\x=2\left(loại\right)\end{matrix}\right.\)
c: Ta có: \(\left(x^2-4\right)-\left(x-2\right)\left(3-2x\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2-3+2x\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(3x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)