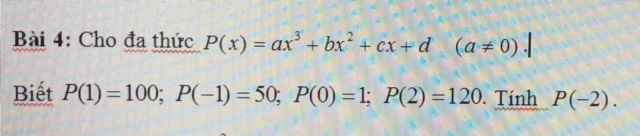Ta có: \(\left\{{}\begin{matrix}P\left(1\right)=100\\P\left(-1\right)=50\\P\left(0\right)=1\\P\left(2\right)=120\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b+c+d=100\\-a+b-c+d=50\\d=1\\8a+4b+2c+d=120\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b+c=99\\-a+b-c=49\\8a+4b+2c=119\\d=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=74\\d=1\\a+c=25\\8a+2c=-29\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=74\\d=1\\2a+2c=25\\8a+2c=-29\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=74\\d=1\\-6a=54\\a+c=25\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-9\\b=74\\c=34\\d=1\end{matrix}\right.\)
Vậy: \(P\left(x\right)=-9x^3+74x^2+34x+1\)
\(\Leftrightarrow P\left(-2\right)=-9\cdot\left(-8\right)+74\cdot4+34\cdot\left(-2\right)+1\)
\(\Leftrightarrow P\left(-2\right)=301\)