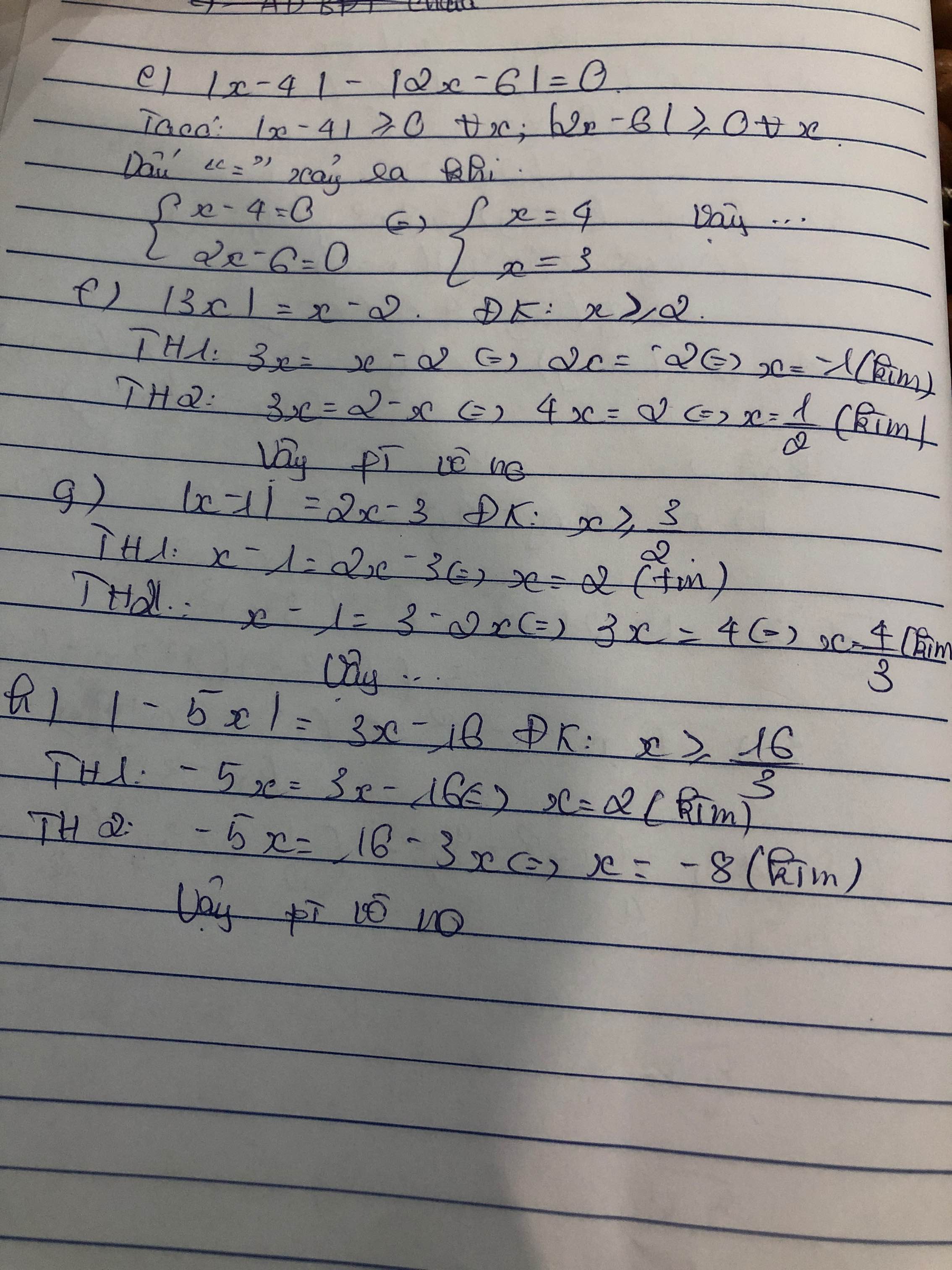Question

Answer 1

Lời giải:

e.

$|x-4|-|2x-6|=0$

$\Leftrightarrow |x-4|=|2x-6|$

$\Leftrightarrow x-4=2x-6$ hoặc $x-4=6-2x$

$\Leftrightarrow x=2$ hoặc $x=\frac{10}{3}$

f.

$x-2=|3x|\geq 0\Rightarrow x\geq 2\Rightarrow |3x|=3x$. PT trở thành:

$3x=x-2$

$\Leftrightarrow x=-1$ (vô lý vì $x\geq 2$)

Vậy pt vô nghiệm

g.

$2x-3=|x-1|\geq 0\Rightarrow x\geq \frac{3}{2}$

$\Rightarrow |x-1|=x-1$. PT trở thành:

$2x-3=x-1\Leftrightarrow x=2$ (thỏa mãn)

Vậy........

h.

$3x-16=|-5x|\geq 0\Rightarrow x\geq \frac{16}{3}$

$\Rightarrow |-5x|=5x$. PT trở thành:

$5x=3x-16\Leftrightarrow x=-8$ (vô lý vì $x\geq \frac{16}{3}$)

Vậy pt vô nghiệm.

Answer 2

Answer 3

e) PT \(\Leftrightarrow\left|x-4\right|=\left|2x-6\right|\)

          \(\Leftrightarrow\left[{}\begin{matrix}x-4=2x-6\\x-4=6-2x\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{10}{3}\end{matrix}\right.\)

  Vậy ...

f) ĐK: \(x\ge2\)

PT \(\Leftrightarrow\left[{}\begin{matrix}3x=x-2\\3x=2-x\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{1}{2}\end{matrix}\right.\) (Loại)

  Vậy phương trình vô nghiệm

g) ĐK: \(x\ge\dfrac{3}{2}\)

PT \(\Leftrightarrow\left[{}\begin{matrix}x-1=2x-3\\x-1=3-2x\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{4}{3}\left(loại\right)\end{matrix}\right.\)

  Vậy ...

h) ĐK: \(x\ge\dfrac{16}{3}\)

PT \(\Leftrightarrow\left[{}\begin{matrix}-5x=3x-16\\-5x=16-3x\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-8\end{matrix}\right.\)  (Loại)

  Vậy phương trình vô nghiệm

  

Answer 4

f) Ta có: |3x|=x-2

\(\Leftrightarrow\left[{}\begin{matrix}3x=x-2\left(x\ge0\right)\\3x=2-x\left(x< 0\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x-x=-2\\3x+x=2\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-1\left(loại\right)\\x=\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\)

g) Ta có: \(\left|x-1\right|=2x-3\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=2x-3\left(x\ge1\right)\\x-1=3-2x\left(x< 1\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-2x=-3+1\\x+2x=3+1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}-x=-2\\3x=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\left(nhận\right)\\x=\dfrac{4}{3}\left(loại\right)\end{matrix}\right.\)