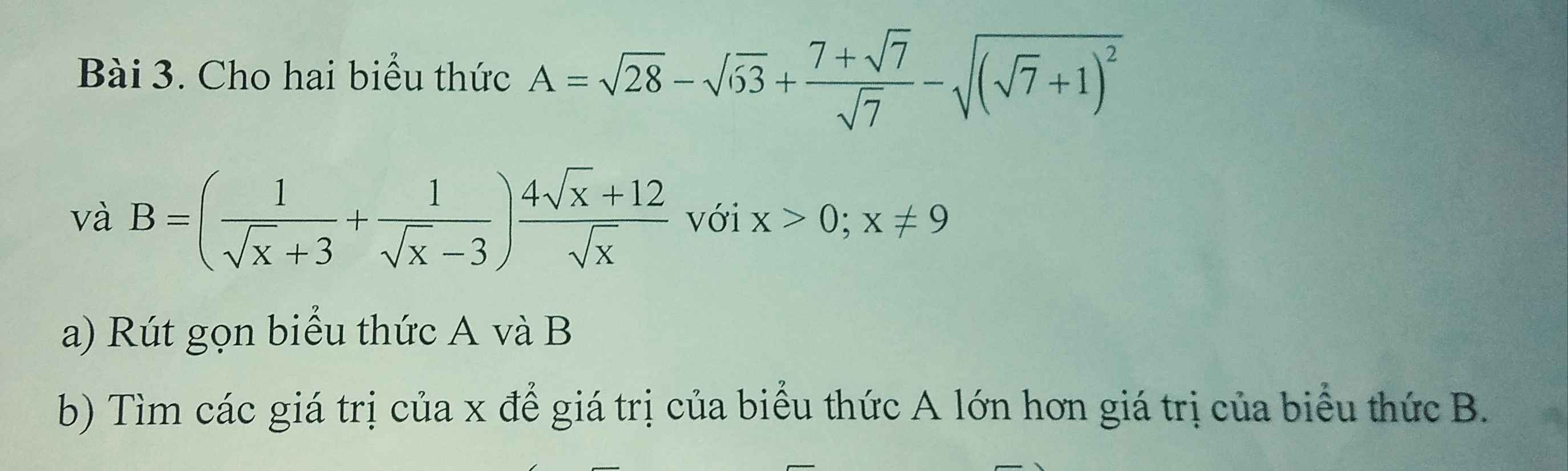a) Ta có: \(A=\sqrt{28}-\sqrt{63}+\dfrac{7+\sqrt{7}}{\sqrt{7}}-\sqrt{\left(\sqrt{7}+1\right)^2}\)
\(=2\sqrt{7}-3\sqrt{7}+\sqrt{7}+1-\sqrt{7}-1\)
\(=-\sqrt{7}\)
Ta có: \(B=\left(\dfrac{1}{\sqrt{x}+3}+\dfrac{1}{\sqrt{x}-3}\right)\cdot\dfrac{4\sqrt{x}+12}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}+3+\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{4\left(\sqrt{x}+3\right)}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}\cdot4}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{8}{\sqrt{x}-3}\)
b) Để \(A\ge B\) thì \(-\sqrt{7}\ge\dfrac{8}{\sqrt{x}-3}\)
\(\Leftrightarrow-\sqrt{7}\left(\sqrt{x}-3\right)\ge8\)
\(\Leftrightarrow\sqrt{x}-3\le\dfrac{-8\sqrt{7}}{7}\)
\(\Leftrightarrow\sqrt{x}\le\dfrac{21-8\sqrt{7}}{7}\)(vô lý)