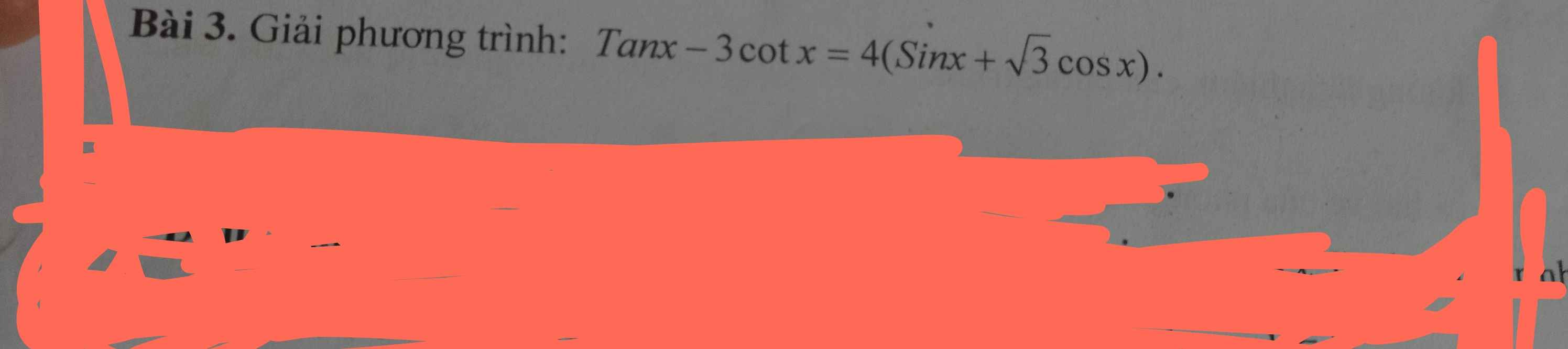Đk:\(x\ne\dfrac{k\pi}{2};k\in Z\)
Pt \(\Leftrightarrow\dfrac{sinx}{cosx}-\dfrac{3cosx}{sinx}=4\left(sinx+\sqrt{3}cosx\right)\)
\(\Leftrightarrow\dfrac{\left(sinx-\sqrt{3}cosx\right)\left(sinx+\sqrt{3}cosx\right)}{cosx.sinx}=4\left(sinx+\sqrt{3}cosx\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+\sqrt{3}cosx=0\\\dfrac{sinx-\sqrt{3}cosx}{cosx.sinx}-4=0\end{matrix}\right.\)
TH1: \(sinx+\sqrt{3}cosx=0\Leftrightarrow sin\left(x+\dfrac{\pi}{3}\right)=0\)
\(\Leftrightarrow x=-\dfrac{\pi}{3}+k\pi,k\in Z\)
TH2:\(\dfrac{sinx-\sqrt{3}cosx}{cosx.sinx}=4\)
\(\Leftrightarrow sinx-\sqrt{3}cosx=4cosx.sinx\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{3}\right)=sin2x\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{3}+k2\pi\\x=\dfrac{4\pi}{9}+\dfrac{k2\pi}{3}\end{matrix}\right.\) (\(k\in Z\))
Vậy \(\left[{}\begin{matrix}x=-\dfrac{\pi}{3}+k\pi\\x=\dfrac{4\pi}{9}+\dfrac{k2\pi}{3}\end{matrix}\right.\) (\(k\in Z\)