Dựng hình thang ABCD (AB//CD), biết ba cạnh : AD = 2cm, CD = 4cm, BC = 3cm và đường chéo AC = 5cm
Ôn tập cuối năm phần hình học

Hướng dẫn giải
Thảo luận (1)

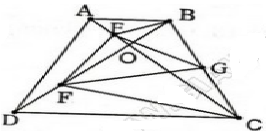
Cho hình thang ABCD (AB // CD) có hai đường chéo cắt nhau ở O và tam giác ABO là tam giác đều. Gọi E, F, G theo thứ tự là trung điểm của các đoạn thăng OA, OD và BC. Chứng minh rằng tam giá EFG là tam giác đều ?
Hướng dẫn giải
Thảo luận (1)

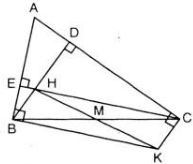
Tam giác ABC có các đường cao BD, CE cắt nhau tại H. Đường vuông góc với AB tại B và đường vuông góc với AC tại C cắt nhau ở K. Tam giác ABC phải có điều kiện gì thì tứ giác BHCK là :
a) Hình thoi
b) Hình chữ nhât
Hướng dẫn giải
Thảo luận (1)

Cho hình bình hành ABCD. Các điểm M, N theo thứ tự là trung điểm của AB, CD. Gọi E là giao điểm của AN và DM, K là giao điểm của BN và CM. Hình bình hành ABCD phải có điều kiện gì để tứ giác MENK là :
a) Hình thoi
b) Hình chữ nhật
c) Hình vuông
Hướng dẫn giải
Thảo luận (2)

Tứ giác MBND là hình bình hành.
(MB// = ND)
Lại có MN // BC (vì MBCN là hình bình hành).
EK // CD (vì EK là đường trung bình của ∆CDM).
a) Để MENK là hình thoi thì hình bình hành MENK phải có hai đường chéo vuông góc. Tức là MN ⊥ EK.
Suy ra BC ⊥ CD.
Vậy ABCD phải là hình chữ nhật.
b) Để MENK là hình chữ nhật thì hình bình hành MENK phải có hai đường chéo bằng nhau. Tức là MN = EK.
Mà MN = BC, EK = \(\dfrac{1}{2}\) CD suy ra:
BC = \(\dfrac{1}{2}\) CD.
c) Để MENK là hình vuông thì MENK phải vừa là hình thoi vừa là hình chữ nhật. Tức là hình bình hành ABCD phải là hình chữ nhật có:
\(BC=\dfrac{1}{2}DC\)

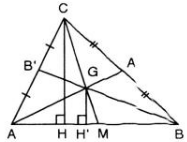
Trong tam giác ABC, các đường trung tuyến AA' và BB' cắt nhau ở G. Tính diện tích tam giác ABC biết rằng diện tích tam giác ABG bằng S ?
Hướng dẫn giải
Thảo luận (1)
Lời giải

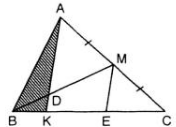
Cho tam giác ABC và đường trung tuyến BM. Trên đoạn BM lấy điểm D sao cho \(\dfrac{BD}{DM}=\dfrac{1}{2}\). Tia AD cắt BC ở K. Tìm tỉ số diện tích của tam giác ABK và tam giác ABC ?
Hướng dẫn giải
Thảo luận (1)
Lời giải

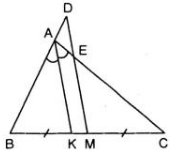
Cho tam giác ABC (AB < AC). Tia phân giác của góc A cắt BC ở K. Qua trung điểm M của BC kẻ một tia song song với KA cắt đường thẳng AB ở D, cắt AC ở E. Chứng minh BD = CE ?
Hướng dẫn giải
Thảo luận (1)
Lời giải

Trên hình 151 cho thấy có thể xác định chiều rộng BB' của khúc sông bằng cách xét hai tam giác đồng dạng ABC và AB'C'. Hãy tính BB' nếu AC = 100m, AC' = 32m, AB' = 34m
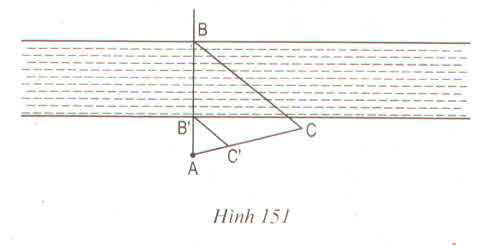
Hướng dẫn giải
Thảo luận (1)

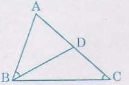
Cho tam giác ABC có AB < AC, D là một điểm nằm giữa A và C.
Chứng minh rằng :
\(\widehat{ABD}=\widehat{ACB}\Leftrightarrow AB^2=AC.AD\)
Hướng dẫn giải
Thảo luận (2)
Lời giải
Ta chứng minh hai chiều:

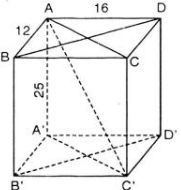
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 12cm, AD = 16cm, AA' = 25cm
a) Chứng minh các tứ giác ACC'A, BĐ'B' là hình chữ nhật
b) Chứng minh rằng \(AC'^2=AB^2+AD^2+AA'^2\)
c) Tính diện tích toàn phân và thể tích của hình hộp chữ nhật
Hướng dẫn giải
Thảo luận (1)
Lời giải






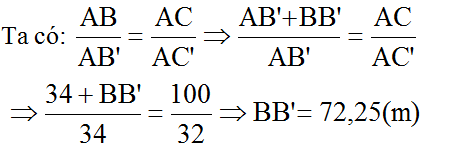
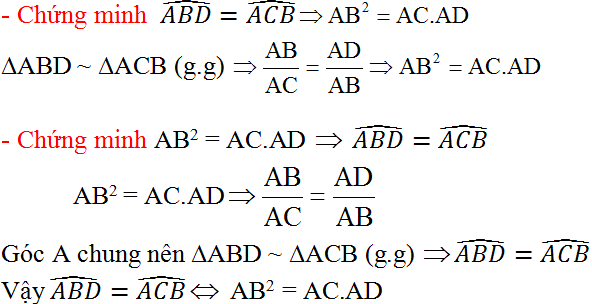


Dựng đoạn thẳng CD = 4cm.
- Dựng hai đường tròn (C, 5cm) và (D, 2cm) cắt nhau tại A.
- Dựng đường tròn (C, 2cm) và đường tròn (A, 4cm) cắt nhau tại B.
Đường thẳng AB kéo dài cắt đường tròn (C, 2cm) tại điểm B' (ngoài điểm B đã kể ở trên)
Các tứ giác ABCD và AB'CD là những hình thang thỏa mãn đề bài.
Chứng minh: Vì B thuộc đường tròn (A, 4cm) nên AB = 4cm.
ΔABC = ΔDCA (AB = CD = 4cm, AD = BC = 2cm, AC chung) do đó góc BAC = góc DCA là cặp so le trong ta có: AB // CD.
Tứ giác ABCD có AB // CD, AD = 2cm, CD = 4cm, BC = 2cm là hình thang thỏa mãn yêu cầu, AB'CD cũng là hình thang thỏa mãn yêu cầu vì AB' // CD, AD = 2cm, CD = 4cm, CB' = 2cm.