Ôn tập cuối năm môn Đại số

Điều kiện cần và đủ của tam giác ABC vuông tại A là các cạnh của nó thỏa mãn hệ thức :

a² + b² = c²

(a, b, c độ dài các cạnh theo thứ tự đối diện các đỉnh A, B, C)

Quy tắc xét dấu một nhị thức dựa trên định lí :

“Nhị thức f(x) = ax + b (a≠0) có dấu cùng với hệ số a khi x lấy giá trị trong khoảng và trái dấu với hệ số a khi x lấy các giá trị thuộc khoảng ”.

Áp dụng: Ta lập bảng xét dấu của vế trái f(x) của bất phương trình:

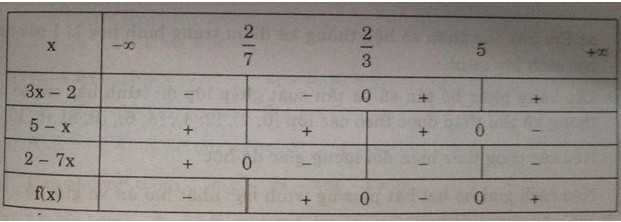
Tập nghiệm của bất phương trình:

Cách nhận biết đa thức

\(f\left(x\right)=ax^2+bx+c\)

Có nghiệm hay vô nghiệm

Lập \(\Delta\) ( đọc là delta )

\(\Delta=b^2-4ac\)

Nếu \(\Delta< 0\) : đa thức vô nghiệm

Nếu \(\Delta\ge0\) : đa thức có nghiệm

Nếu \(\Delta>0\) : đa thức có hai nghiệm

\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}\)

\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}\)

- Các tính chất của bất đẳng thức:

TC1. ( Tính chất bắc cầu)

TC2. (Quy tắc cộng)

A < B <=> A + C < B + C

TC3. (Quy tắc cộng hai bất đẳng thức dùng chiều)

TC4. (Quy tắc nhân)

TC5. (Quy tắc nhân hai bất đẳng thức)

TC6. (Quy tắc lũy thừa, khai căn)

Với A, B > 0, n ∈ N^* ta có:

A < B <=> Aⁿ < Bⁿ

A < B <=> .

- Áp dụng tính chất: 0 < an < bⁿ với n ∈ N^*

Xét: 2³⁰⁰⁰ = (2³)¹⁰⁰⁰

3²⁰⁰⁰ = (3²)¹⁰⁰⁰

Ta có: 0<2³<3² ⇒ (2³)¹⁰⁰⁰ < (3²)¹⁰⁰⁰

Do đó: 2³⁰⁰⁰ < 3²⁰⁰⁰

1.Công thức cộng:

sin(x+y)=sinx.cosy+cosx.siny

sin(x-y)=sinx.cosy-cosx.siny

cos(x+y)=cosxcosy-sinxsiny

cos(x-y)=cosxcosy+sinxsiny

tan(x+y)=\(\dfrac{tanx+tany}{1-tanx.tany}\)

tan(x-y)=\(\dfrac{tanx-tany}{1+tanx.tany}\)

2.Công thức nhân đôi:

sin2x=2sinx.cosx

cos2x=cos²x-sin²x=1-2sin²x=2cos²x-1

tan2x=\(\dfrac{2tanx}{1-tan^2x}\)

3. Công thức hạ bậc:

sin²x=\(\dfrac{1-cos2x}{2}\)

cos²x=\(\dfrac{1+cos2x}{2}\)

tan²x=\(\dfrac{1-cos^2x}{1+cos^2x}\)

4. Công thức biến đổi tích thành tổng:

cosx.cosy=\(\dfrac{1}{2}\)[cos(x-y)+cos(x+y)]

sinx.siny=\(\dfrac{1}{2}\)[cos(x-y)-cos(x+y)]

sinx.cosy=\(\dfrac{1}{2}\)[sin(x-y)+sin(x+y)]

5. Công thức biến đổi tổng thành tích:

cosx+cosy=2cos\(\dfrac{x+y}{2}\).cos\(\dfrac{x-y}{2}\)

cosx-cosy=2sin\(\dfrac{x+y}{2}\).sin\(\dfrac{x-y}{2}\)

sinx+siny=2sin\(\dfrac{x+y}{2}\).cos\(\dfrac{x-y}{2}\)

sinx-siny=2cos \(\dfrac{x+y}{2}\).sin \(\dfrac{x-y}{2}\)

\(\left\{{}\begin{matrix}2X+Y\ge1\left(1\right)\\X-3Y\le1\left(2\right)\end{matrix}\right.\)

*Giải 2X+Y-1=0

cho đi qua 2 điểm và thử điểm O(0;0) vào (1) và loại đi phần k thỏa mãn

*Tương tự giải X-3Y-1=0

*Lấy giao (1) và (2)

a) Tập xác định của f(x) :

A = {x ∈ R | x² + 3x + 4 ≥ 0 và -x² + 8x – 15 ≥ 0}

- x² + 3x + 4 có biệt thức Δ = 3² – 16 < 0

Theo định lí dấu của tam thức:

x² + 3x + 4 ≥ 0 ∀x ∈R

-x² + 8x – 15 = 0 ⇔ x₁ = 3, x₂ = 5

-x² + 8x – 15 > 0 ⇔ 3 ≤ x ≤ 5 ⇒ A = [3, 5]

b) A/B = [3, 4]

R\(A\B) = (-∞, 3) ∪ (4, +∞)